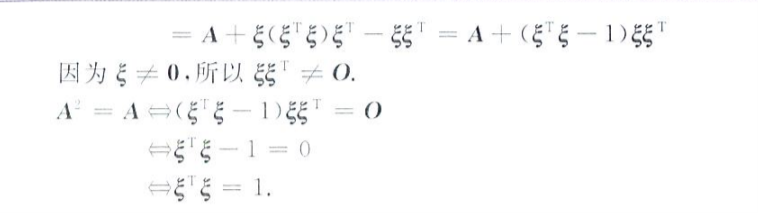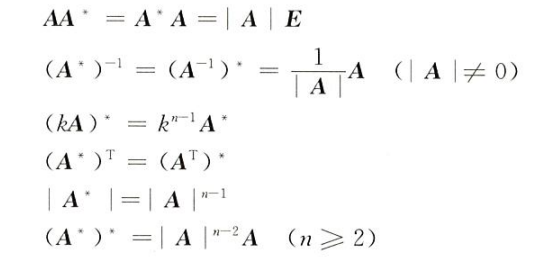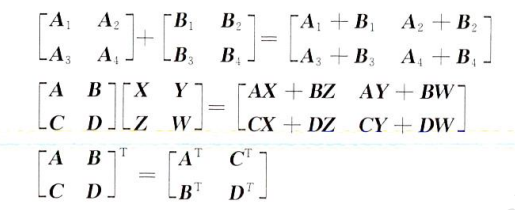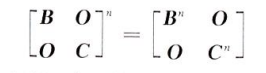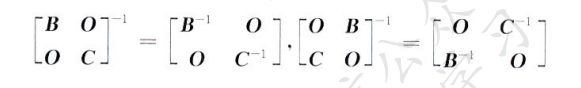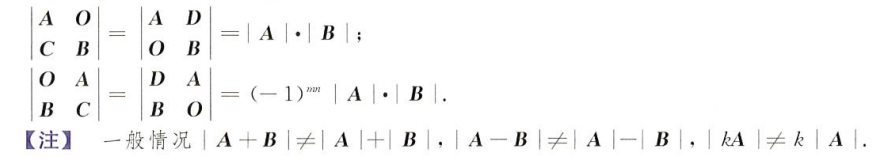矩阵的概念及计算
始终牢记,线性代数是一门研究有限维空间内线性映射的学科
矩阵分类
矩阵A,其行列式记作|A|,当然只有方阵才有对应行列式
| 矩阵分类 | 矩阵特征 |
|---|
mxn矩阵 | m 行 n 列的矩阵 |
n阶方阵 | n 行 n 列的矩阵,有对应行列式|A| |
| 零矩阵 | 所有元素全为 0 的矩阵(区分于行列式,行列式实际上就是一个数值,其为 0 和矩阵为 0 是完全不同的概念) |
| 同型矩阵 | 行列数相等,即尺寸一样的矩阵 |
单位阵E | 主对角线上全为 1,其余位置全为 0 的矩阵,有AE = EA = A |
| 数量阵 | 即为单位阵的数乘,kE |
| 对角阵 | 除主对角线上其余位置全为 0 的矩阵 |
| 转置矩阵 | 行列位置变换(区分与行列式,行列式行列互换值不变) |
| 对称阵 | 自身与其转置矩阵完全相等 |
| 反对称阵 | 其转置矩阵等于自身的负矩阵,即数乘-1就为其转置阵 |
| 矩阵多项式 | 对于多项式f(x) = a0 + a1x + a2x^2 + ... + anx^n,将其自变量更换为矩阵A,即得到对应的矩阵多项式 |
各类矩阵的性质
单位阵
AE=EA=A
对角阵
AB=BA=[b1a100b2a2]<=>a1b1=b1a1−−−−−−−−−−−−−−−−−−−An=[a100a2]n=[a1n00a2n]
转置阵
(A+B)T=AT+BT(AB)T=BTAT(AT)T=A
矩阵多项式,涉及矩阵的阶乘(也就是乘法)
f(A)=amAm+am−1Am−1+...+a1A+a0
矩阵的运算
加法:仅限于同型矩阵,就是每一个位置的元素相加
数乘:常数 k 乘以矩阵 A,即将常数 k 乘到 A 的每一个元素上
乘法:只有当左矩阵的列数等于右矩阵的行数时才能相乘,结果为一个新的矩阵
- 单行乘以单列得到一个一维矩阵,就是一个数值
- 就是左矩阵的行元素依次乘上右矩阵的列元素再相加,得到一个新元素
- 乘法是矩阵运算中最重要也是最基本的,他不满足交换律,没有消去律,有零因子(即两个不为 0 的矩阵可以相乘得到零矩阵)
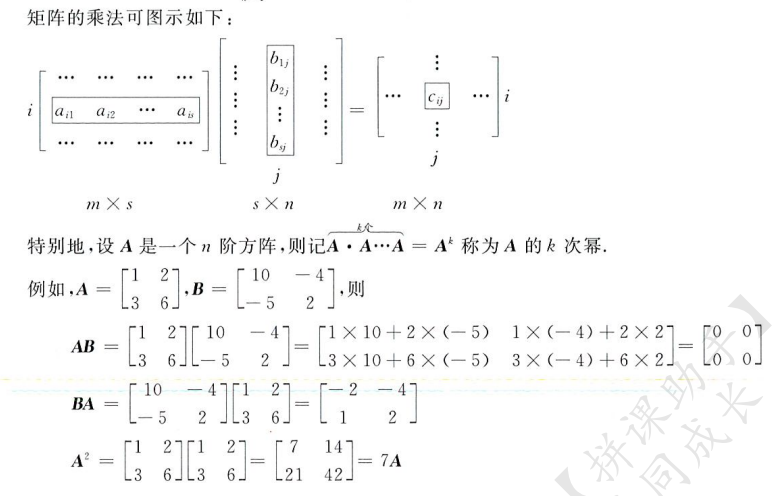
矩阵的乘法满足结合律,但注意左乘和右乘一定不能交换位置
AB+AC=A(B+C)
数乘满足交换律,结合律
kmA=mkAkA+kB=k(A+B)
这里矩阵满足结合律,意味着下式成立
(A+B)(C+D)=AC+AD+BC+BD
矩阵基础运算
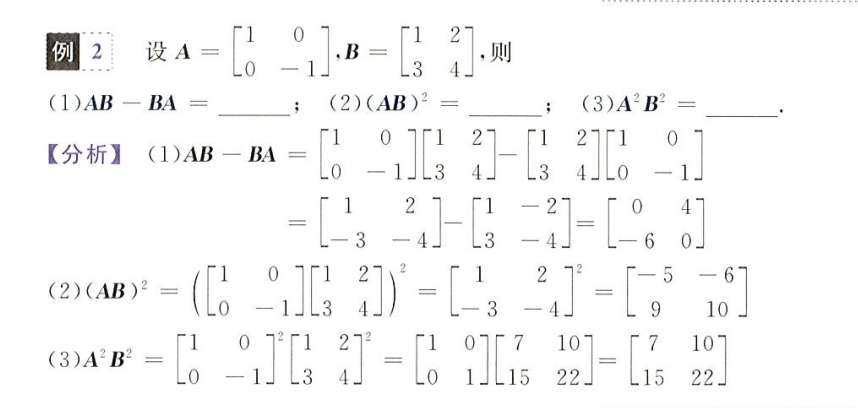
利用矩阵结合律求解方程

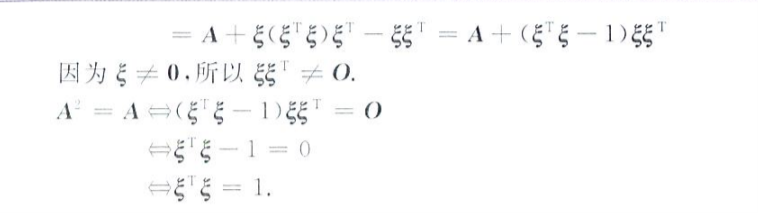
矩阵和方程组
用矩阵表示方程组,向量乘以向量

用矩阵计算表示方程组,如对于方程组
⎩⎨⎧a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2......an1x1+an2x2+...+annxn=bn
将其系数矩阵提出,有
A=a11a21...an1a12a22an2.........a1na2nann
未知数矩阵提出,有
X=x1x2...xn
由矩阵乘法,得
Ax=b1b2...bn=B
将系数矩阵A模块化处理,令其为
A=[A1,A2,...,An]
就有
A1x1+A2x2+...+Anxn=B
伴随矩阵和可逆矩阵
伴随矩阵定义及性质
用于求解逆矩阵
伴随矩阵,回顾一下代数余子式,对于行列式|A|,其在i,j的代数余子式为
Aij=(−1)i+jMij
其中Mij为行列式|A|除去第 i 行第 j 列的新行列式的值
对于方阵A,其对应行列式为|A|,其伴随矩阵为
A∗=A11A12...A1nA21A22A2n.........An1An2Ann 其中每一个元素都是对应转置位置的代数余子式,每行的代数余子式竖着放构成的矩阵
举个栗子

伴随矩阵的性质:建议一个个推一下
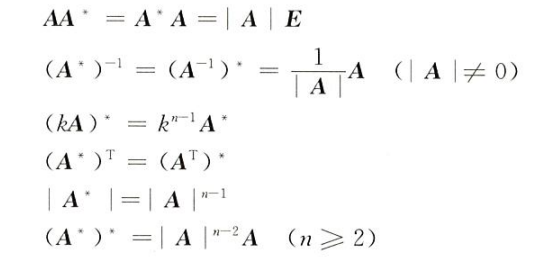
可逆矩阵定义及性质
重要矩阵,逆矩阵和原矩阵相乘可得单位阵
可逆矩阵,若
AB=BA=E
则说A和B互为可逆矩阵,记作
A−1=BB−1=A
n 阶矩阵可逆的充要条件

这里一定是不能出现线性相关的向量,很自然的,若有线性相关,则必有一行可以转化为零向量,该行矩阵相乘结果恒为 0,不可能出现单位阵 E
逆矩阵的运算性质

求解逆矩阵
对角矩阵的逆
a1000a2000a3−1=1/a10001/a20001/a3
一维矩阵的逆
∣a∣−1=∣a1∣
定义法:直接找出矩阵B使得AB = E,则B就是A的逆矩阵


公式法
A−1=∣A∣1A∗ 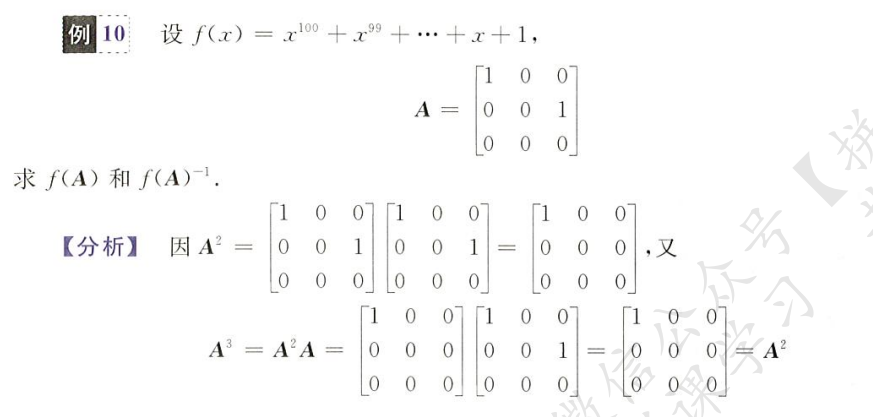

行变换法
(A∣E)→初等行变换(E∣A−1) 
分块矩阵法
[A00B]−1=[A−100B−1]−−−−−−−−−−−[0BA0]−1=[0A−1B−10]
结合矩阵乘法结合律考察


初等变换和初等矩阵
初等变换与初等矩阵的概念
初等变换
- 倍乘初等矩阵:用非零常数 k 乘以矩阵 A 的某一行每个元素
- 互换初等矩阵:两行交换位置
- 倍加初等矩阵:用某行的 k 倍加在另一行上
初等矩阵即由单位阵 E 经由一次初等变换得到的矩阵
等价矩阵:A 经由有限次初等变换得到矩阵 B,则称 A 和 B 互为等价矩阵
初等变换与初等矩阵的性质
初等变换后的矩阵和原先矩阵等价,初等矩阵乘以矩阵等同于在该矩阵上做初等矩阵相应的初等变换
初等矩阵的转置仍是初等矩阵
初等矩阵均是可逆矩阵,且其逆矩阵均是初等矩阵
用初等矩阵 P 乘以矩阵 A,相当于对 A 作出相应的初等行变换,如
[1101][1324]
相当于把第二个矩阵的第一行加在第二行上,得
[11+322+4]
如果是右乘,即
[1324][1101]
相当于把第二列加在第一列上,得
[1+23+424]
也就是说,左乘对应行变换,右乘对应列变换
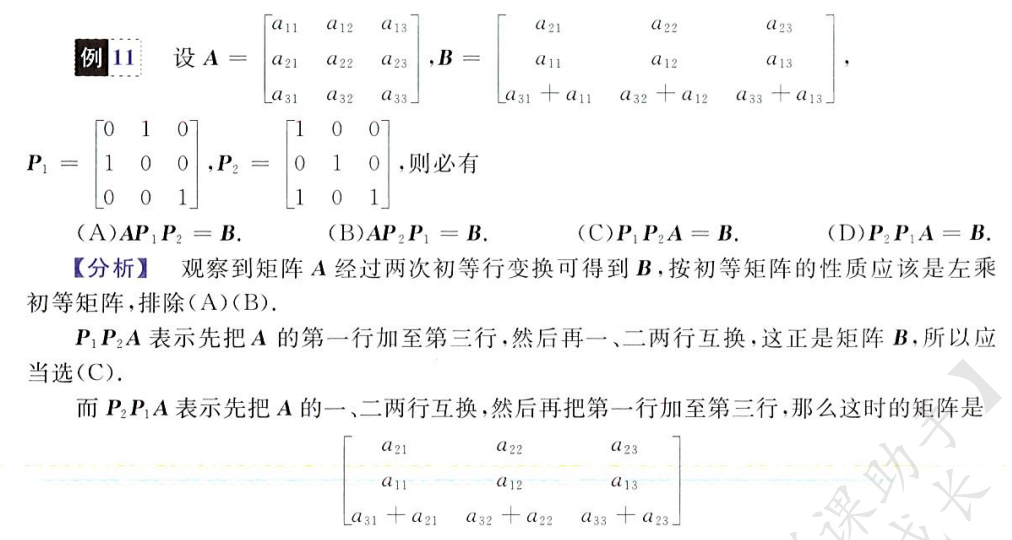
利用初等矩阵进行初等变换,几个栗子

行阶梯矩阵、行最简矩阵
由于初等变换后的矩阵和之前的等价,于是我们选择一种简便的矩阵,行阶梯矩阵或行最简矩阵代替原先的复杂矩阵,进行一系列计算
主元:矩阵每个行向量的第一个非零元素称作该行的主元
行阶梯矩阵:全零行位于矩阵底部,非零行的主元列指标 j 随行指标 i 的增大而严格递增,就是说,越往下的主元必须越靠右,这样的矩阵为行阶梯矩阵
行最简矩阵:每个行向量的主元为 1,每个主元所在列向量除主元外均为 0 的行阶梯矩阵

求行最简矩阵方法
- 先从上往下,从左往右将主元所在列之下元素全化为 0
- 再从下往上,从右往左将主元所在列之上元素全化为 0
求行变换对应初等矩阵:(A|E) ——> (B|P),则有AP = B,P即为A行变换到B的初等矩阵


分块矩阵
降阶的感觉,分块的概念最早出现在拉普拉斯行列式
分块矩阵定义
不同于行列式,行列式的分块是为了简化计算,如凑出全 0 阵,利用拉普拉斯进行求解
矩阵的分块更加自由,行列不受限制,由于不同的需求,同一个矩阵可以用迥异的方法分块,如

每一个小块称作分块矩阵的子矩阵
分块矩阵运算
加减、乘法和转置
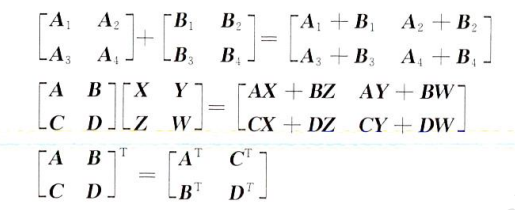
阶乘运算
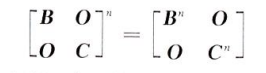
逆运算
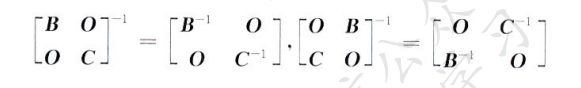
举个栗子
- 证明矩阵可逆:对应行列式不为 0
- 根据矩阵的运算以及逆矩阵的定义证明两矩阵互相可逆

通过分块可以有效地简化计算

分的随意一点,注意副对角线矩阵逆运算的性质

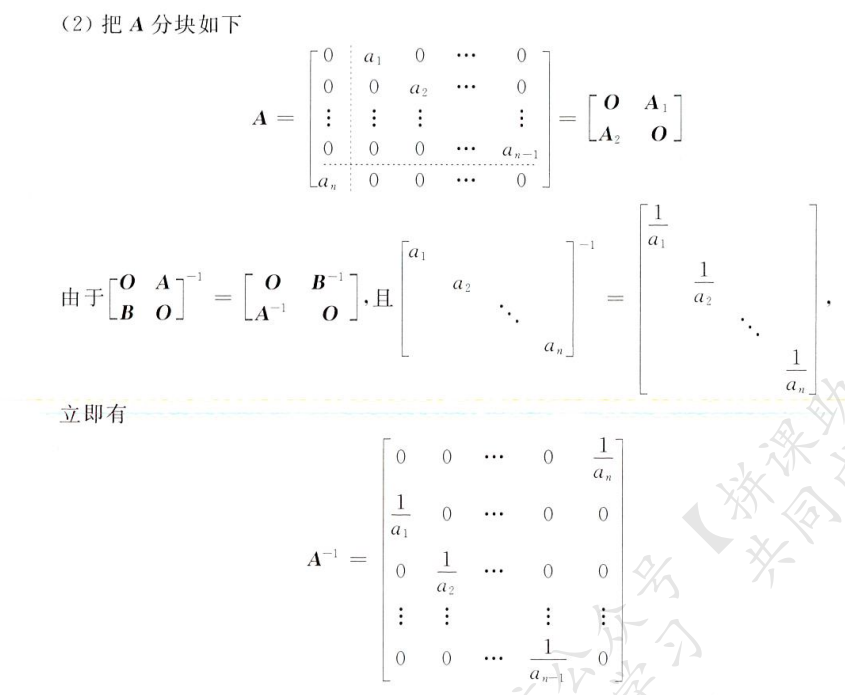
方阵的行列式
方阵行列式的性质:设有 n 阶矩阵 A
转置:转置矩阵行列式等于原矩阵
数乘:k乘在矩阵的每个元素上,行列式每行提出一个k,共n行
∣kA∣=kn∣A∣
乘法和阶乘
∣AB∣=∣A∣∣B∣∣A2∣=∣A∣2
伴随:理解不了
∣A∗∣=∣A∣n−1
逆运算:行列式是一个数,指-1为其倒数
∣A−1∣=∣A∣−1
分块矩阵
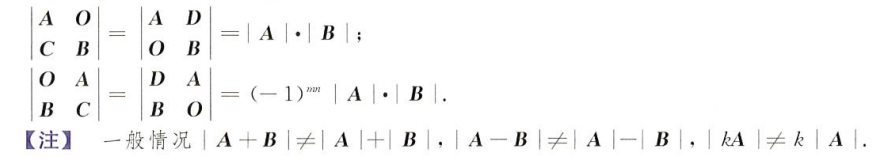
举俩栗子

这里注意一个逆矩阵和伴随阵的相互替换
A∗=∣A∣A−1