线性方程组

线性方程组及相关概念

基本概念

线性方程组，就是多元一次方程组，如下列方程组

$$\begin{cases} a_{11}x_1+...+a_{1n}x_n = b1\\ a_{21}x_1+...+a_{2n}x_n = b2\\ ...\\ a_{n1}x_1+...+a_{nn}x_n = bn\\ \end{cases}$$

化为向量（矩阵）乘法的形式

$$Ax = b$$

当b为零向量时，为齐次线性方程组，否则为非齐次线性方程组

对于任意一个非齐次方程组，令其b向量为零向量，得到其对应的齐次方程组，也称作非齐次方程组的导出组

系数矩阵A的秩，其实就是方程组中有效方程的个数，如同我熟知的，一个两元一次方程组，两个不同的方程可以解出确定解，这里也一样，当r(A) = n，方程组的解将被唯一确定

• 若为齐次方程组，则说明该方程只有唯一的一个全零解
• 若为非齐次方程组，说明该方程通解只由唯一一个特解构成

解方程组的步骤

化简矩阵：初等行变换

• 系数矩阵
• 增广矩阵

判定解的形式：根据矩阵秩的大小和未知数的数量判断解的情况

• 齐次满秩：唯一零解
• 齐次非满秩：基础解系存在n-r个向量
• 非齐次满秩：唯一特解
• 非齐次非满秩：存在一个特解和对应齐次方程组n-r个向量构成的通解，二者共同构成非齐次的通解

解方程：通常通过正交的方式确定自由项，确定n-r个自由项的值，解出方程，得到通解

齐次线性方程组

基础解系和通解

对于齐次线性方程组，当r(A) < n时，此时方程组的解将有无穷个（因为一定存在n-r(A)个不被确定约束的变量，我称之为自由项），通过自定义线性无关的自由项，可以解出n-r(A)个不同的解向量，这些解向量共同构成原方程的基础解系，而齐次线性方程组的通解，即为基础解系的任一线性表出

简单说，秩表示有效方程的数量，r 个有效方程约束了 r 个变量，剩下的 n-r 个变量自由发挥，通过线性无关排列，可以表示出任一符合该方程组的向量组合

求解齐次线性方程组

解齐次方程组

• 首先，化行最简系数矩阵
• 第二，确定自由项
• 第三，解方程，得到基础解系
• 最后，添上常数系数k，得到通解

举两个栗子

可以发现，其实解齐次线性方程组的步骤非常固定

关于解的构成，牢记n-r(A)为自由项的个数，即为基础解系向量的个数

非齐次线性方程组

增广矩阵和导出组

对于非齐次方程组

$$Ax = b$$

其对应的增广矩阵如下

$$\overline{A} = (A|b)$$

只有当

$$r(A) = r(\overline{A})$$

时，非齐次方程组才存在有效解

上述非齐次方程组对应导出组（齐次线性方程组）

$$Ax = 0$$

当系数矩阵秩等于增广矩阵秩时，确定非齐次方程组有解，根据r(A)和未知数数量n的比较，可以得知通解的构成

• 当r(A) = n时，原方程组存在唯一特解
• 当r(A) < n时，原方程组通解由非齐次特解 + 对应齐次通解构成

求解非齐次线性方程组

求解大体分为两步，每一大步都要经过化简矩阵、判定解形式和解方程的步骤

• 求解特解
• 求解导出组通解

举两个梨子

仍可以发现，解非齐次方程组的方法也很固定，化简增广矩阵，判断秩的大小确定自由项个数，确定一个特解，解对应齐次方程组通解，糅合一下得到原方程组通解

要注意的是这里的化简方法，涉及到之前的初等行变换，灵活一点，通常通解不唯一

解的个数和增广矩阵秩的关系

非齐次线性方程组的通解和其对应导出组通解的关系

方程组的应用

可交换矩阵

可交换的概念，对于矩阵乘法，有

$$AB = BA$$

则说矩阵A和B可交换

通过线性方程组求解可交换矩阵

就是矩阵各个位置元素乘出来，列等式，联立方程组，通过解方程组求得各个位置元素的具体值（通解）

求解矩阵方程

通过线性方程组求解矩阵方程

这里不能用传统的求逆的方式求解矩阵乘法方程（很显然这里的矩阵都不可逆），只能用解线性方程组通解的形式求解每个位置的元素值

线性相关和线性表出

线性相关及线性表出和线性方程组通解的关系

线性相关和解情况的联系

将线性表出的系数视作未知数，联立线性方程组，求解线性表出的系数，表示出确定的线性表出

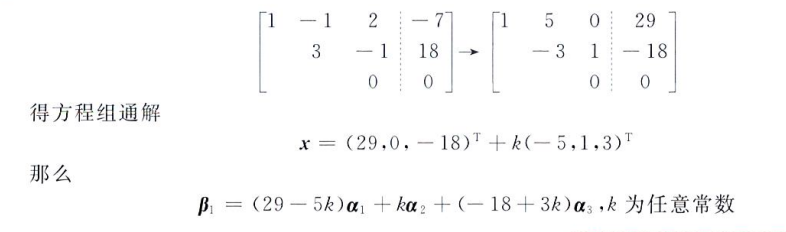
已知解系求方程组

逆天