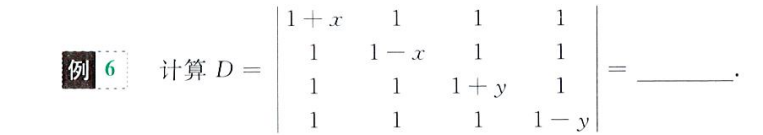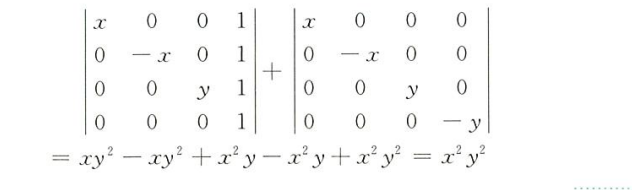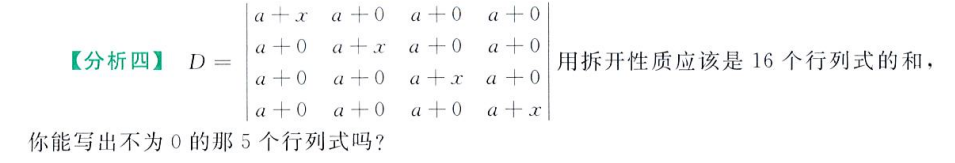行列式

行列式概念及性质

行列式定义

行列式是一个数，他是不同行不同列元素乘积的代数和

如三阶行列式的对角线法计算法

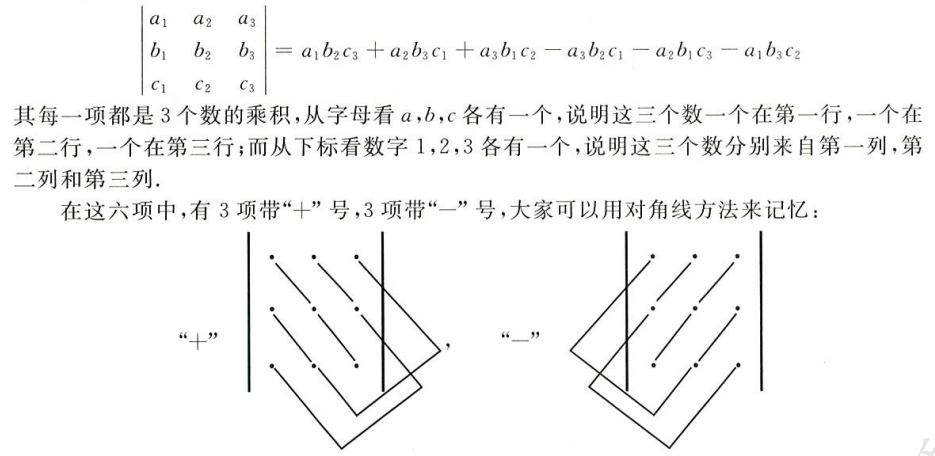
逆序和逆序数

对于4321，其每位上的逆序分别为3,2,1，因为4>3>2>1，所以对于 4 来说，后三位均是逆序，其逆序自然为 3，同理，在这个序列中，3 的逆序为 2，2 的逆序为 1

逆序数指的是序列所有元素逆序之和，如上述序列逆序数为3+2+1 = 6，为偶数

• 逆序数为偶数，序列为偶排列
• 否则为奇排列

展开公式法计算行列式

$$|A| = \sum_{j_1j_2...j_n}(-1)^{\tau(j_1j_2...j_n)}a_{1j_1}a_{2j_2}...a_{nj_n}$$

其中

$$\tau(j_1j_2...j_n)$$

为序列j1 j2 ... jn的逆序数，就是说，若序列为偶排列，则为正，否则为负

注意对角线法可以列出所有的行列式序列，每个序列的符号通过逆序数来确定

行列式性质

所有行都可以等价于列，因为行列置换后行列式等价，行等于列

$$|A| = |A^T|$$

两行互换位置，行列式值变号

$$\left | \begin{matrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{matrix} \right | = -\left | \begin{matrix} a_{12}&a_{11}\\ a_{22}&a_{21} \end{matrix} \right |$$

某整行的公因子可以提出

$$\left | \begin{matrix} ka_{11}&a_{12}\\ ka_{21}&a_{22} \end{matrix} \right | = k\left | \begin{matrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{matrix} \right |$$

存在某行全为 0 的行列式值为 0

$$\left | \begin{matrix} a_{11}&a_{12}&0\\ a_{21}&a_{22}&0\\ a_{31}&a_{32}&0 \end{matrix} \right | = 0$$

存在某两行线性相关，行列式值为 0

$$\left | \begin{matrix} a_{11}&a_{12}&ka_{12}\\ a_{21}&a_{22}&ka_{22}\\ a_{31}&a_{32}&ka_{32} \end{matrix} \right | = 0$$

其中第二列和第三列线性相关，A2 = kA3

行列式的线性加法不改变值，什么是线性加法？就是某一行的整数倍加到另一行上，如

$$\left | \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{matrix} \right | = \left | \begin{matrix} a_{11}&a_{12}&a_{13}+ka_{12}\\ a_{21}&a_{22}&a_{23}+ka_{22}\\ a_{31}&a_{32}&a_{33}+ka_{32} \end{matrix} \right |$$

这也侧面印证了，若两行线性相关，则行列式值为 0 的结论，因为线性相关的行一定能通过线性加法得到全为 0 的行，从而行列式值一定为 0

行列式的拆分

$$\left | \begin{matrix} a_{11}&a_{12}&b_{1}+c_{1}\\ a_{21}&a_{22}&b_{2}+c_{2}\\ a_{31}&a_{32}&b_{3}+c_{3} \end{matrix} \right | = \left | \begin{matrix} a_{11}&a_{12}&b_{1}\\ a_{21}&a_{22}&b_{2}\\ a_{31}&a_{32}&b_{3} \end{matrix} \right | + \left | \begin{matrix} a_{11}&a_{12}&c_{1}\\ a_{21}&a_{22}&c_{2}\\ a_{31}&a_{32}&c_{3} \end{matrix} \right |$$

行列式计算

行列式按行展开

余子式

$$|M_{ij}| = |A|去掉第i行第j列所对应行列式$$

代数余子式

$$(-1)^{i+j}|M_{ij}|$$

行列式按第 i 行展开，m 为行列式 A 的列数

$$|A| = \sum_{j=1}^{m}a_{ij}(-1)^{i+j}|M_{ij}|$$

行展开，就是行列式一整行的元素乘上其对应的代数余子式的总和，等于原行列式的值（列同理）

注意一整行的元素乘上另一行的代数余子式的总和恒为零

栗子一

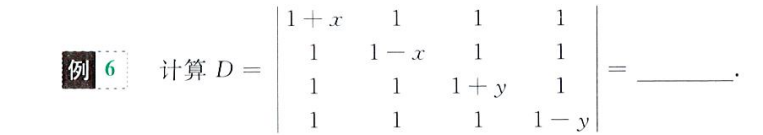
可以通过倍加凑出只有一个非零元素的行，然后按行展开简化计算

栗子二

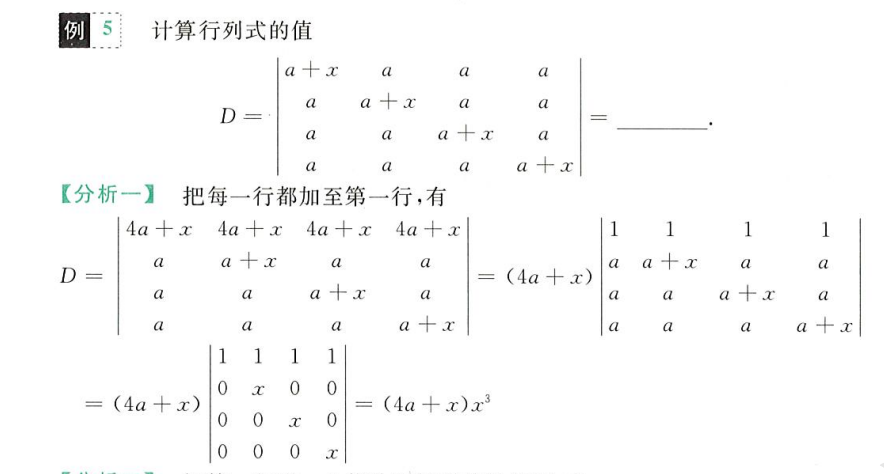
通过行列式方程按行展开解未知数

拆分法

通过拆开矩阵元素，删去含全零行的行列式，计算保留项，以此简化计算（行列式来自于栗子一）

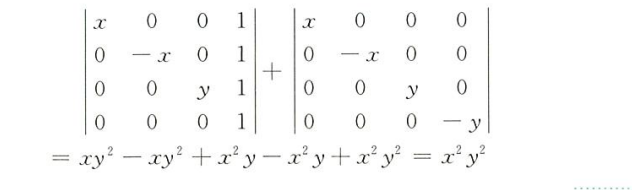
栗子二的拆分法

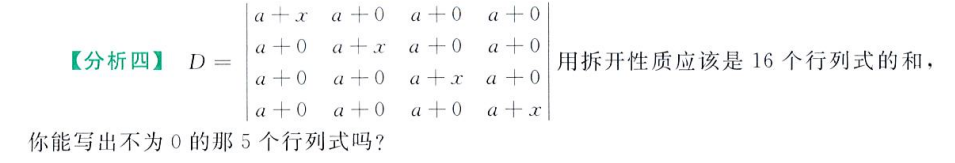
爪形处理

就是通过倍加凑出上下三角行列式或斜对角线行列式，以简化计算

上三角

上/下三角行列式（对角线行列式）

$$\left | \begin{matrix} a_{11}&a_{12}&a_{13}\\ 0&a_{22}&a_{23}\\ 0&0&a_{33} \end{matrix} \right | = a_{11}a_{22}a_{33}$$

所谓的爪形处理，就是凑上三角行列式以简化计算，行列式来自栗子一

栗子二的爪形处理

副对角线

副对角线行列式

$$\left | \begin{matrix} 0&0&a_{13}\\ 0&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{matrix} \right | = (-1)^{\frac{n(n-1)}{2}}a_{13}a_{22}a_{31}$$

拉普拉斯

上三角行列式和副对角线行列式的分块矩阵形式

拉普拉斯行列式

$$\left | \begin{matrix} A&0\\ 0&B \end{matrix} \right | = |A|\,|B| \\-------\\ \left | \begin{matrix} 0&A\\ B&0 \end{matrix} \right | = (-1)^{mn}|A|\,|B|$$

其中m和n分别为行列式A和B的阶数

范德蒙行列式

范德蒙行列式

$$\left | \begin{matrix} 1&1&1\\ x_{1}&x_{2}&x_{3}\\ x_{1}^2&x_{2}^2&x_{3}^2 \end{matrix} \right | = (x_3-x_2)\times(x_3-x_1)\times(x_2-x_1)$$

推广到 n 阶，即为

$$\prod_{1\leq j<i\leq n}(x_i-x_j)$$

通过数学归纳法可以证明

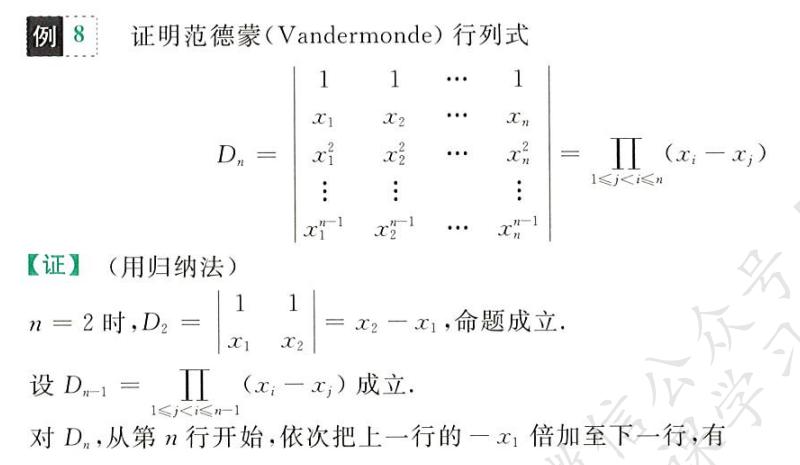
范德蒙行列式计算

$$\begin{aligned} |A| &= \left | \begin{matrix} 1&1&1\\ 2&-1&-3\\ 4&1&9 \end{matrix} \right | \Rightarrow x_1 = 2,x_2=-1,x_3=-3\\ &=(x_3-x_1)(x_3-x_2)(x_2-x_1)\\ &=(-5)(-2)(-3)\\ &=-30 \end{aligned}$$

我发现行列式等式证明的题，是不是喜欢用数学归纳法，确实比较适配

总结来说

行列式计算

• 化简展开：按照行列式的性质，一般使用线性加法得到足够多的 0，然后按行展开，降阶行列式，然后使用对角线法直接计算
• 凑特殊行列式求解：拉普拉斯行列式，上三角行列式，范德蒙行列式

解方程

• 首先一定涉及行列式的计算，这是前提，将行列式化简和凑特殊行列式计算出来，然后视作一个一元多次方程求解未知数λ

证明题：通常来说，是证明一个等式行列式为 n 阶时始终成立，可以考虑用数学归纳法，请参考范德蒙行列式的证明，从n-1阶推导n阶成立得证

行列式解非齐次方程组

克拉默法则

对于非齐次线性方程

$$\begin{cases} a_{11}x_1+...+a_{1n}x_n = b1\\ a_{21}x_1+...+a_{2n}x_n = b2\\ ...\\ a_{n1}x_1+...+a_{nn}x_n = bn\\ \end{cases}$$

克拉默法则：针对线性方程组的系数矩阵，若其系数矩阵对应行列式值不为 0（行列式不存在线性相关的行），说明方程组只有一个唯一解，且解为

$$x_i = \frac{|A_i|}{|A|}$$

其中Ai为第i列替换为B的行列式，如A1为

$$\left | \begin{matrix} b_{1}&a_{12}&...&a_{1n}\\ b_{2}&a_{22}&...&a_{2n}\\ ...\\ b_{n}&a_{n2}&...&a_{nn} \end{matrix} \right |$$

应用到齐次方程组上（即b1=b2=..=bn=0），若其系数行列式值不为 0，则说明其只有一个解，一定是x1=x2=...=xn=0，即只存在全 0 解

相应的，只有当系数行列式值等于 0 时，说明系数行列式存在线性相关的行（行列式性质），齐次方程组才存在非 0 解，也就是说存在线性相关的项

这里的逻辑有点乱，但是是正确的，就是说，行列式为 0，通过行列式性质可知，行列式存在线性相关的行（即ai = kaj），所对应的齐次方程组的解xi和xj就可以不为 0，如

$$a_i = ka_j\,,\,\,x_j = -kx_i \Rightarrow a_ix_i + a_jx_j = 0$$

这样就有了不全为 0 的解

求解非齐次方程组特解：xi = |Ai| / |A|