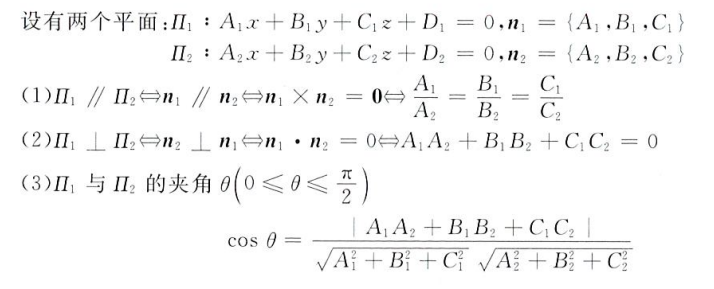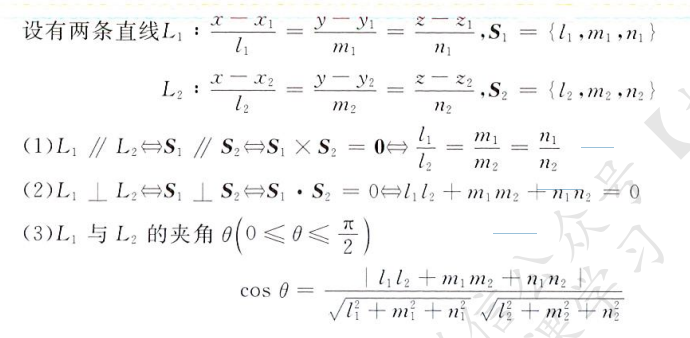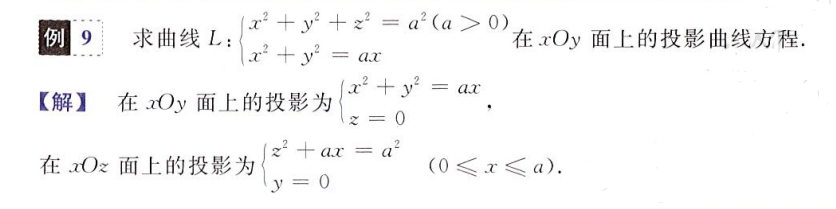向量代数和空间解析几何

向量代数

向量定义

向量定义：和线代保持一致，就是一个高维数，如a = (a1,a2,a3)

特殊向量：单位向量（模为 1），零向量（模为 0）

加法

$$a + b = (a_1+b_1,\,a_2+b_2,\,a_3+b_3)$$

数乘

$$ka = (ka_1,\,ka_2,\,ka_3)$$

向量的所有运算规律和矩阵保持一致

向量乘积

数量积

数量积：就是矩阵乘法，也叫点积，几何意义为向量a在向量b上的投影a'乘以向量b，参考夹角力做，表示向量之间的实际作用效果

$$ab = (a,b) = ab^T = a_1b_1+a_2b_2+a_3b_3$$

模长

$$|a| = \sqrt{aa} = \sqrt{a_1^2+a_2^2+a_3^2}$$

向量夹角

$$cos\alpha = \frac{ab}{|a|\,|b|}$$

通过数量积判定垂直

$$ab = 0 \iff a\bot b \iff cos\alpha = 0\,(\alpha = \frac{\pi}{2})$$

向量积

向量积：记作axb，结果是一个向量 c，该向量垂直于向量 a、b 确定的平面，且数值上有

$$|c| = |a|\,|b|\,sin\alpha\,(\alpha为a,b夹角)$$

实际上是一个右手定则，从向量 a 握向 b，大拇指朝向即为axb向量的方向

在代数上，axb为一个带方向的行列式

$$a\times b = \left | \begin{matrix} i&j&k\\ a_1&a_2&a_3\\ b_1&b_2&b_3 \end{matrix} \right | = (a_2b_3-a_3b_2)i+(a_3b_1-a_1b_3)j+(a_1b_2-a_2b_1)k$$

几何意义

• c 天然是 a b 平面的一条垂线
• 当向量积为 0，说明两向量平行，sinα = 0
• 向量积在数值上（即|c|），等于以向量 a、b 为邻边的平行四边形的面积（平行四边形高为bsinα）

注意叉乘是一个行列式，符合一切行列式运算的规则，如置换两列位置换号，同列的公因子可以提出等等

混合积

三个向量的数量积等于前两个向量的向量积和第三个向量的数量积

$$abc = (a\times b)c = \left [ \begin{matrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3 \end{matrix} \right ]$$

同理，这个混合积满足行列式的运算规则

且有几何意义

• 当abc=0说明平面 ab 的垂线同时垂直于向量 c，于是向量 abc 在同一平面上
• 混合积在数值上等于以向量 a、b、c 为棱的平行六面体体积

空间解析几何

空间平面与直线方程

空间平面抓法向量，空间直线抓方向向量

空间平面方程

一般式，点法式，截距式

平面方程：在三个方向上都是一阶线性，于是是平面，就像二维的一阶线性，一定是直线，而不是曲线

$$Ax+By+Cz = D$$

法向量为

$$n = [\frac{∂f}{∂x},\frac{∂f}{∂y},\frac{∂f}{∂z}] = [A,B,C]$$

三个确定的法向量其实就可以确定一个平面的倾斜角度，再用一个点即可确定任一平面，在一般式里面，用常数 D 来确定这个经过的点

点法式：过(x0,y0,z0)的平面方程

• 法向量为(A,B,C)
• 过点(x0,y0,z0)

法向量和经过的一个点即可确定一个平面

$$A(x-x_0)+B(y-y_0)+C(z-z_0) = 0$$

截距式：过(a,0,0), (0,b,0), (0,0,c)的平面方程

• 法向量同样是确定的，为(1/a, 1/b, 1/c)
• 一定过三个截距点

法向量和经过的一个点确定平面

$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$$

其法向量为(1/a, 1/b, 1/c)

空间直线方程

一般式，对称式，参数式

一般式：两个空间平面的交线确定一条空间直线

$$\begin{cases} A_1x+B_1y+C_1z = D_1\\ A_2x+B_2y+C_2z = D_2 \end{cases}$$

一般式求方向向量：其实就是一个解齐次线性方程组的过程

因为已知两平面方程，可以轻易得到两平面的法向量

$$\beta_1 = (A_1,B_2,C_3)\quad \beta_2 = (A_2,B_2,C_2)$$

因为直线是平面的交线，自然同时位于两个平面上，于是一定垂直于这两条法向量，设l = (x1,x2,x3)，则有

$$\begin{cases} A_1x_1+B_1x_2+C_1x_3 = D_1\\ A_2x_1+B_2x_2+C_2x_3 = D_2 \end{cases}$$

这他妈就是一个齐次线性方程组，其系数矩阵为

$$A = \left [ \begin{matrix} A_1&B_1&C_1\\ A_1&B_2&C_2 \end{matrix} \right ]$$

一定可以解得l的一个基础解系，随便取一个特解即为这条空间直线的方向向量

对称式

$$\frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}$$

其方向向量为(l,m,n)，为什么？？

参数式

$$\begin{cases} x = x_0+lt\\ y = y_0+mt\\ z = z_0+nt \end{cases}$$

其方向向量为(l,m,n)

空间平面、直线间关系

一定要结合线代知识考虑计算

直线、平面的关系

关系：平行、垂直、夹角

直线与平面的关系

平面与平面的关系

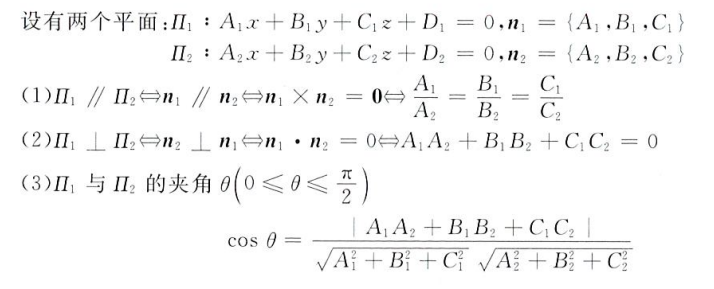
直线与直线的关系

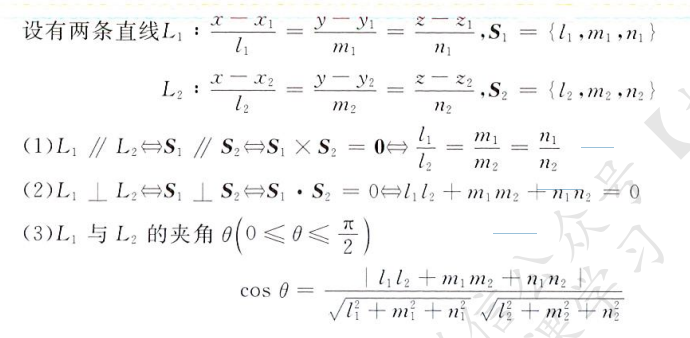
这里的一系列计算可以不严格按照高数的方法，可以采用线代的方式求解齐次线性方程组来判定直线方向

点到直线、平面的距离

就是点积/叉积除以模长之积

点到面的距离：(x0,y0,z0)到Ax + By + Cz + D = D的距离

$$d = \frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$$

点到直线的距离

直线为对称式，过点(x1,y1,z1)，方程为

$$\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$$

点(x0,y0,z0)到直线距离为

$$d = \frac{|\,(x_1-x_0,y-y_0,z-z_0)\times (l,m,n)\,|}{\sqrt{l^2+m^2+n^2}}$$

曲面与空间曲线方程

曲面方程

显函数形式

$$z = f(x,y)\quad (x,y)\in D\subset R^2$$

隐函数形式

$$F(x,y,z) = 0$$

参数方程形式

$$\begin{cases} x = x(u,v)\\ y = y(u,v)\\ z = z(u,v) \end{cases} \quad (u,v)\in D_{uv}\subset R^2$$

空间曲线方程

一般式：两曲面交线

$$\begin{cases} F(x,y,z) = 0\\ G(x,y,z) = 0 \end{cases}$$

参数方程形式

$$\begin{cases} x = x(t)\\ y = y(t)\\ z = z(t) \end{cases} \quad t \in D\subset R^1$$

旋转曲面方程与柱面

旋转面：一条平面曲线绕平面上一条直线旋转

设 L 是yOz平面上一条曲线,其方程是

$$\begin{cases} f(y,z) = 0\\ x = 0 \end{cases}$$

则 L 绕 y 轴旋转所得旋转面方程为

$$f(y，土\sqrt{x^2+z^2})= 0$$

L绕 x 轴旋转所得旋转面方程为

$$f(士\sqrt{x^2+y^2},z)= 0$$

类似地可写出xOy面或xOz面上的曲线绕其所在坐标面上的坐标轴旋转所产生的旋转面方程

柱面：平行于定直线并沿定曲线 П 移动的直线 L 形成的轨迹

淮线为

$$\begin{cases} f(x,y) = 0\\ z = 0 \end{cases}$$

母线平行于 z 轴的柱面方程为 f(x,y) = 0

淮线为

$$\begin{cases} F(x,y,z) = 0\\ G(x,y,z) = 0 \end{cases}$$

母线平行于 z 轴的柱面方程为 F 和 G 消去变量 z 得到的二元方程 H(x,y)

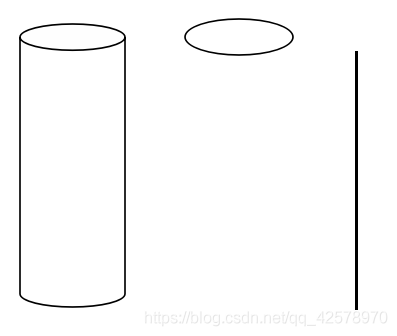
左为柱面，中为淮线，右为母线

投影

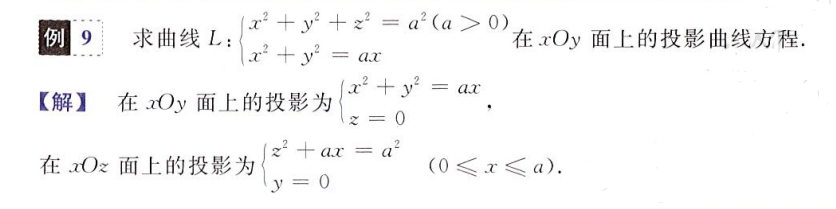
常用二次曲面方程

圆柱面

$$x^2+y^2 = R$$