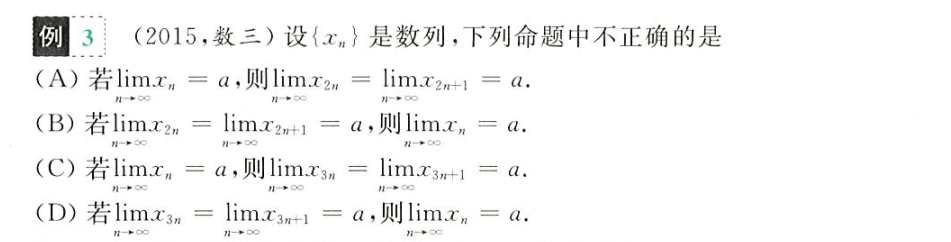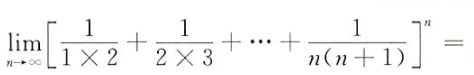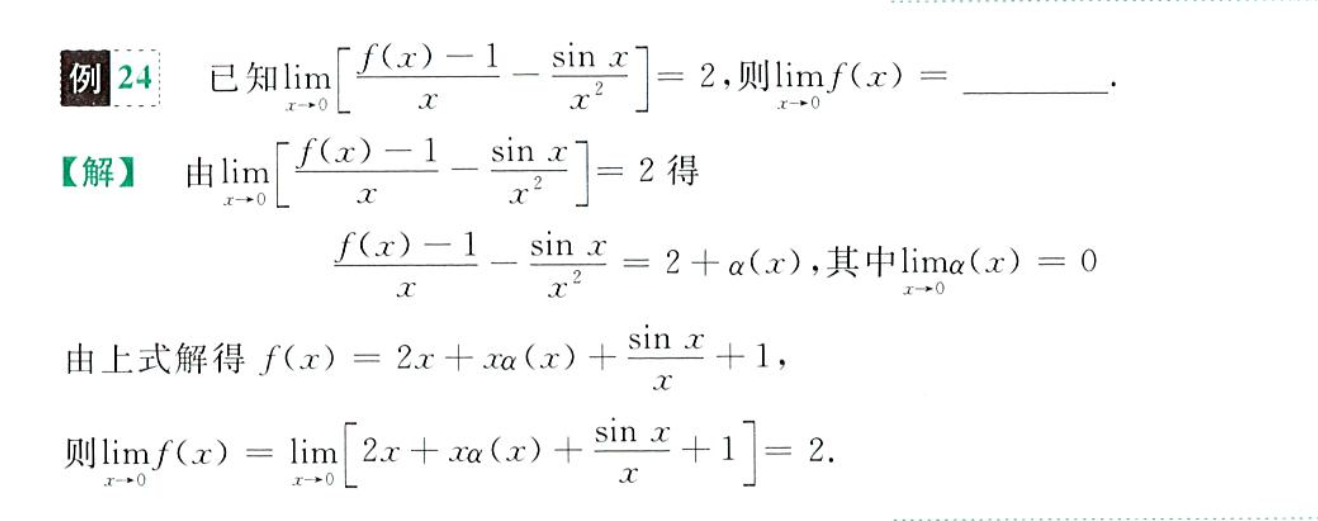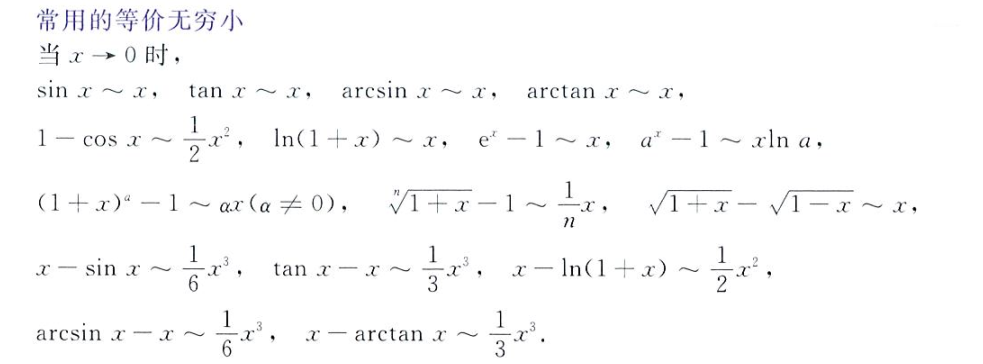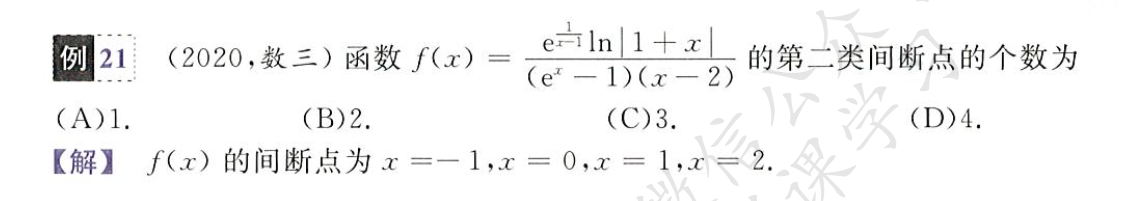函数、极限和连续

函数

函数的定义

复合函数：f[g(x)]，注意g(x)的值域对应f(x)的定义域，f(g(x))的定义域是x的取值范围，但一般规范的是g(x)的取值范围

反函数：注意类似y=x^2这样的函数并没有反函数，因为一个y对应多个x，并不符合函数要求（但可以说是曲线）

$$f^{-1}[f(x)] = x\\ f[f^{-1}(x)] = x$$

基本初等函数

• 幂函数：x 为底数
• 指数函数：x 为指数
• 对数函数
• 三角函数：正割等于余弦分之一
  • sin-cos：正弦余弦，定义域R，值域[-1,1]
  • tan-cot：正切余切，注意分母不为零，值域R
  • sec-csc：正割余割，注意分母不为零，值域(-∞,-1]∪[1,+∞)
• 反三角函数
  • arcsin：反正弦，定义域[-1,1]，值域[-π/2, π/2]
  • arccos：反余弦，定义域[-1,1]，值域[0,π]
  • arctan：反正切，定义域R，值域(-π/2,π/2)
  • arccot：反余切，定义域R，值域(0,π)

这里 tan 函数的定义域是 R 去掉分母为 0 的部分，而反函数 arctan 定义域为 R（因为 tan 函数值域为 R），但值域只能在 tan 函数的一个周期内，不然就不会满足函数定义，其余反三角函数同理

三角函数

转换

$$sin^2x+cos^2x=1\\ sec^2x=1+tan^2x\\ csc^2x=1+cot^2x\\ arcsinx+arccosx=\pi/2\\ arctanx+arccotx=\pi/2\\$$

导数

$$(sinx)'=cosx\\ (cosx)'=-sinx\\ (tanx)'=sec^2x\\ (cotx)'=-csc^2x\\ (arcsinx)'=x\\$$

函数的性质

单调性；奇偶性；周期性；有界性

奇偶

• 奇函数乘除奇函数，偶数个结果为偶，奇数个结果为奇
• 偶函数乘除偶函数结果总是为偶
• 奇函数乘除偶函数结果为奇
• 奇函数若在 x=0 有定义，则 y 一定为 0

周期

• 若自变量变化速度增加两倍（系数乘以 2），则周期减半
• 周期函数相加减，新函数也具有周期性，且周期为两个周期的最小公倍数

有界：多涉及放缩或极大极小值判断

极限

极限概念及性质

数列极限

定义

$$\exist N\in R,\,当\,n>N,\,有\,|a_n-b|<\varepsilon\in Z^{+}\\ 则\,b\,为数列\,a_n\,的极限$$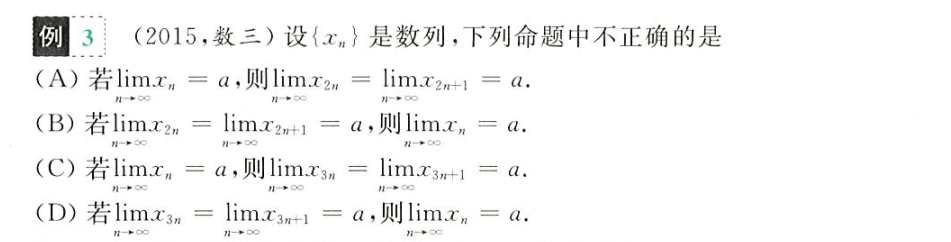

3n 和 3n+1 没有包含所有情形，还应加上 3n+2

同理，若为 4n，则必须要有4n+1, 4n+2, 4n+3才能充分证明

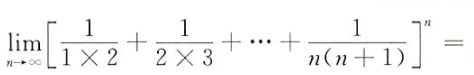
首先是一个经典的1/(2x3) = 1/2-1/3转换消去中间项

第二用到对数转换和等价无穷小

$$\lim_{n\rightarrow\infty}\,\,log_a(1+\frac{1}{n}) = \frac{1}{n\times lna}$$

将中括号中内容加对数得T = ln(1+1/t)^t，将指数t提出，将对数部分1+1/t利用等价无穷小转换为1/t， 求得T = 1，还原对数得原式为e，再对指数e^m进行极限运算，得出最终结果

函数极限

函数无穷极限，定义

$$\lim_{x\rightarrow\infty}f(x) = \lim_{x\rightarrow+\infty}f(x) = \lim_{x\rightarrow-\infty}f(x)$$

极限不存在情形

$$\lim_{x\rightarrow\infty}f(x) = \infty\\ \lim_{x\rightarrow+\infty}f(x) \not= \lim_{x\rightarrow-\infty}f(x)$$

• 不管有没有绝对值，一定要分段讨论，分别判断左右极限，最终才能得出结论

• 当 x 趋于 0 时，除了绝对值，诸如

  $$e^{\frac{1}{x}}\,,\,arctan\frac{1}{x}$$
  均要左右求极限，很明显左右极限不等

函数在有限值的极限，和无穷极限同理，一样分左右（不等或任有一个等于无穷则极限不存在），自变量趋近的值为有限值 A

左右不等的极限

• 表达式带绝对值，自变量趋于 0

• e - ∞型

  $$\lim_{x\rightarrow0}e^{\frac{1}{x}}\,,\, \lim_{x\rightarrow\infty}e^x\,,\, \lim_{x\rightarrow\infty}e^{-x}$$

• arctan - ∞ 型

  $$\lim_{x\rightarrow0^-}arctan\frac{1}{x} = -\frac{\pi}{2}\\ \lim_{x\rightarrow0^+}arctan\frac{1}{x} = \frac{\pi}{2}\\$$

极限的保号性

• xn > 0 恒成立，只能推出其极限 A >= 0（并非 A > 0）
• 若极限 A > 0，可以推出 xn > 0 恒成立

向答案靠拢，令 ε = a/2，通过不等式以及保号性推算结果，不要臆想

无穷小量和无穷大量

无穷小和无穷大

• 有界量（如 4sinx + 3）和无穷小的乘积为无穷小

• k 阶无穷小，若

  $$lim\frac{\beta}{\alpha^k}=c\in R$$
  则称 β 是 α 的 k 阶无穷小（β 远比 α 要小）

• 高阶无穷小：若相除为 0，说明分子比分母更快趋于 0，分子是分母的高阶无穷小；相对的，分母是分子的低阶无穷小

上题用到的几个等价无穷小

$$cosx-1\sim-\frac{1}{2}x^2\\ e^{x}-1\sim x\\ ln(1+x)\sim x\\ {^n}\sqrt{1+x}-1\sim \frac{x}{n}$$

连续洛必达中根据分子/分母趋于 0 解未知数

• 这里继续洛可以得到 -6b = a^3，根据这里的 a-1 = 0 可解出答案

• 三个等价无穷小

极限值与无穷小的关系

$$limf(x) = A <=> f(x) = A+\alpha(x)\\ li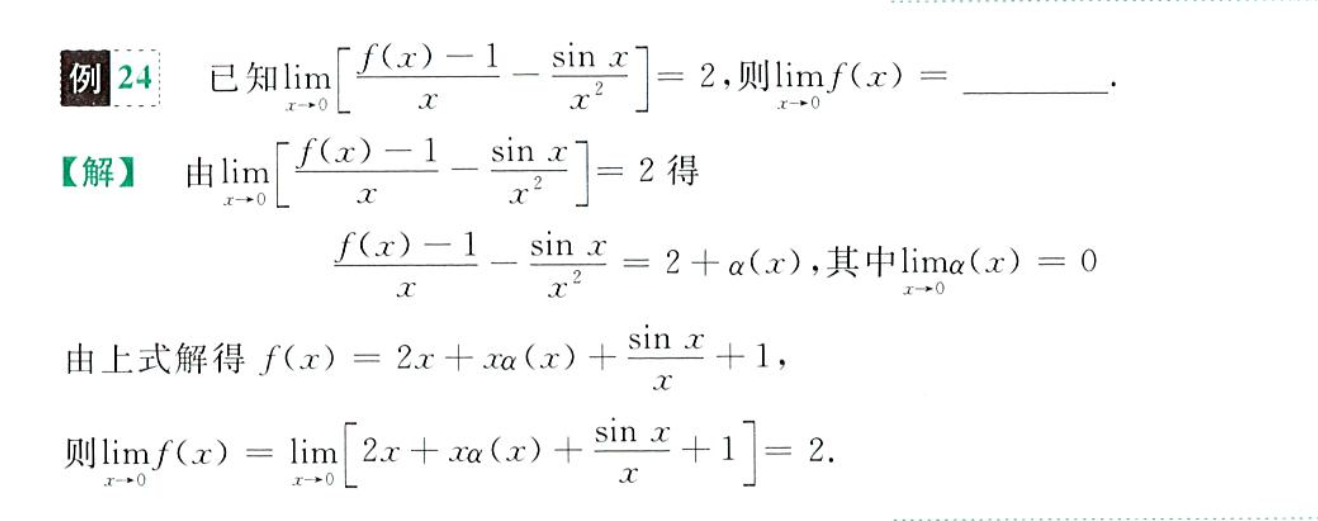m\,\alpha(x) = 0$$

无穷大：无穷大乘以非零常数仍为无穷大

无穷大的比较：通过除法以及洛必达法则可证明

注意无界变量和无穷大量的区别，如对于数列xn = {1,0,3,0,...,2n+1,0,...}，其在奇数位为 x，在偶数位恒为 0，当 n->∞ 时，你不能说他是一个无穷大量，而是一个无界变量

极限计算方法

重中重

朴素求极限

常用结论

对于根号-无穷型极限

• 根号有理化
• 提出公因子，将根号中转化为 0（跟号外为无穷）（注意计算）
• 带入极限

$$\lim_{x\rightarrow+\infty}(\sqrt{x^2+x+1}-\sqrt{x^2-x+1})$$

• 先有理化，再提公因子，比较稳妥
• 提公因子的时候还要注意符号

两个重要极限

1、0/0 型：一般可以直接洛

$$\lim_{a\rightarrow0}\frac{sina}{a} = 1$$

经典错误

2、1-∞ 型：常用于幂指函数，刻意去凑 1

$$\lim_{a\rightarrow0}(1+a)^{1/a} = e$$

注意两个重要极限均有趋于 0 的限制，在无穷小时才成立

对于幂指函数，还可以直接采用把指数化为 e 的对数指数的形式求解极限，如

$$\lim_{x\rightarrow0}(\frac{1+2^x}{2})^\frac{1}{x} = \lim_{x\rightarrow0}\,e^{\frac{1}{x}ln(\frac{1+2^x}{2})}\\ e^{lnx} = x$$

回顾一下指数、对数求导

$$(2^x)' = 2^x\times ln2\\ (log_2x)' = \frac{1}{x\times ln2}$$

幂指函数求解极限一般方法

等价无穷小

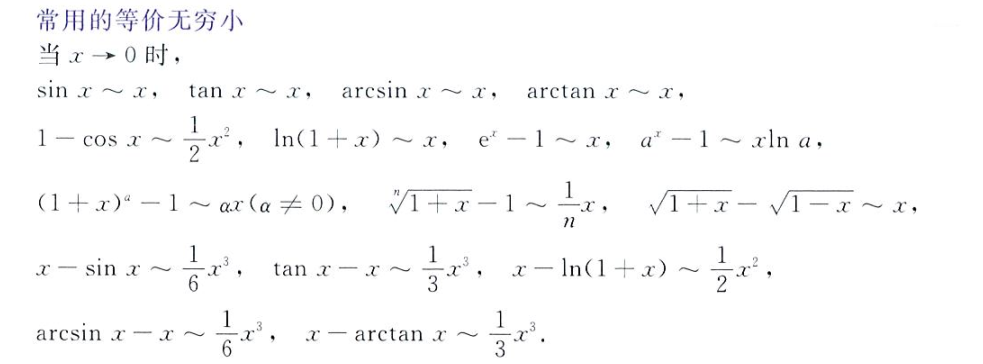
这个故事告诉我们不能一味的追求替换，当算则算

无穷小的和差项不要轻易拆开，尽力化为乘积项统一约分

证明题：证明两个极限等价，即证明这两个极限相除为 1

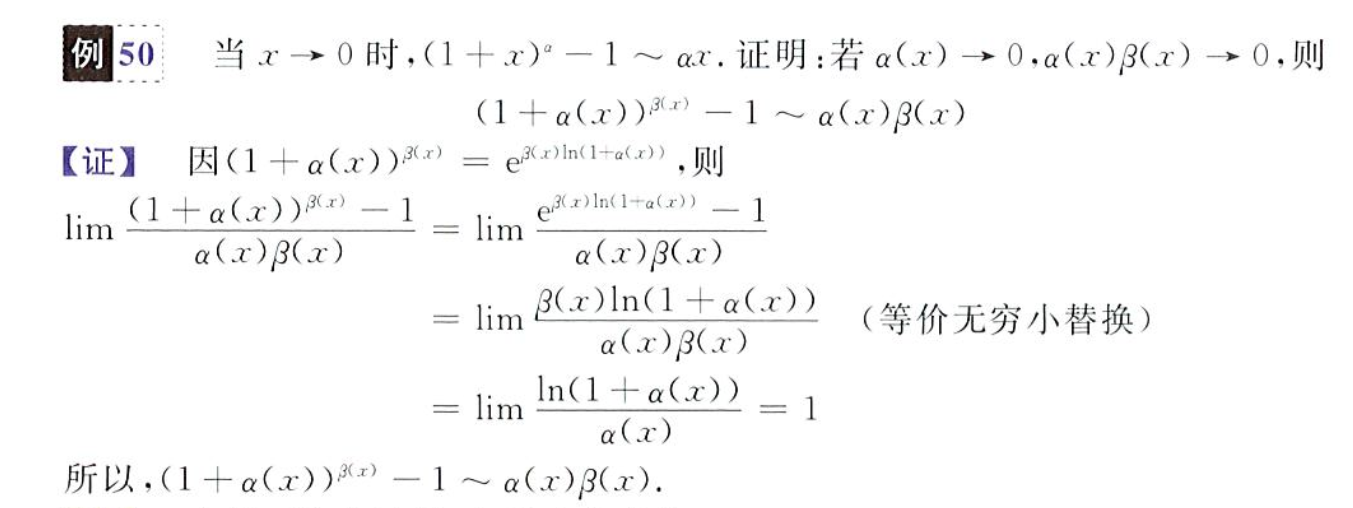
不要怕化出 1，a+b不如a/b+1

夹逼准则 - 放缩

$$若\,g(x)\leq f(x)\leq h(x)\,,\, lim\,g(x) = lim\,h(x) = A\\ 则\,lim\,f(x)=A$$

涉及一个放缩，需要亿点灵感

• 阶乘直接展开
• 乘法注意大于一和小于 1 的部分，分开看

分式永远比乘式要好用

取整函数（向下取整），向上取整同理

单调有界数列极限准则

单调递增数列有界 <=> 必有极限

• 证明单调有界：数学归纳法

• 令

  $$lim\,x_n = a\\ lim\,x_{n+1}=lim\,f(x_n)=f(a)=a$$
  因为已经到极限了，xn+1是等于xn的，以此建立等式

怎么说，就是靠一手递推公式列出关于极限的等式反向求解

注意你在观察这个递推公式的时候，应该是能有感觉的，什么感觉呢，就是上下界的感觉，他既然给出这个题，说明肯定是有界的，你譬如

$$x_{n+1} = \sqrt{6+x_n}$$

这样的一看就是有下界，那么有意识地就要往递减上去归纳，又譬如

$$x_{n+1} = \sqrt{6-x_n}$$

这样就是有上界，数学归纳时向递增上靠拢

利用无穷小性质求极限

就是 无穷小乘以有限量 仍为无穷小（即 0），如

$$\lim_{x\rightarrow \infty}\frac{x^2-3x+5}{2x^3}\times(5+cos3x)$$

分母高次，第一项为无穷小，第二项绝对值始终小于等于 6，相乘结果极限为 0

利用函数连续性求极限

即令极限等于函数值，这适用于一切初等函数，若函数连续，则

$$\lim_{x\rightarrow a}f(x) = f(a)$$

在此基础上，可以复合其他连续函数

其实在很多时候自然的就用到了初等函数的连续性，糅杂在朴素求极限的过程中，伴随各种求极限方法同时使用

• 对指数的乘除和对数的加减一定要敏感

泰勒展开

常用泰勒展开式：o(x^n) 指 x 的 n 阶无穷小，意思是该项相对于 x^n 为无穷小（下一阶无穷小）

1. $$e^x = 1+x+\frac{x^2}{2!}+...+\frac{x^n}{n!}+o(x^n)$$
2. $$sinx = x-\frac{x^3}{3!}+...+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n})$$
3. $$cosx = 1-\frac{x^2}{2!}+...+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n})$$
4. $$ln(1+x) = x-\frac{x^2}{2}+...+(-1)^{n-1}\frac{x^n}{n}+o(x^n)$$
5. $$(1+x)^a = 1+ax+\frac{a(a-1)}{2!}x^2+...+\frac{a(a-1)...(a-n+1)}{n!}x^n+o(x^n)$$

其实进一步看，极大无穷小就是把泰勒式的第三阶展开便视作无穷小，当然这只在 x 趋于 0 的时候才成立

洛必达

灵活的在洛必达、无穷小替换、等价变换、直接求值之间转换，不要拘泥于一种方法

• 先判断是否需要换元（转换为除法更好运算，全是乘法不好操作）
• 若有指数，考虑幂指转换
• 时刻注意分子分母有理化和算术变换（如三角函数变换，凑 1）
• 时刻注意是否可以提出极限为常数的项
• 判断是否有等价无穷小
• 碰到僵局尝试考虑洛必达

一些逆天

$$\lim_{x\rightarrow0}\frac{arctanx-sinx}{x^3}=-1/6\\ \lim_{x\rightarrow0}\frac{e^x-e^{-x}-2x}{x-sinx}=2\\ \lim_{n\rightarrow\infty}\,n\,tan\frac{1}{n}=e^{1/3}\\ \lim_{x\rightarrow0}\frac{\sqrt{1+2sinx}-x-1}{x^2}=-1/2\\ \lim_{x\rightarrow0}\frac{e^{x^{2}}-e^{2-2cosx}}{x^4}=1/12\\$$

极限和无穷小的联系，α(x) 是一个虚构的未知的函数，在已知极限中某一项为 0 且不影响极限构成时（如 0-0 就不行），可以单独提出极限然后悄无声息地消去

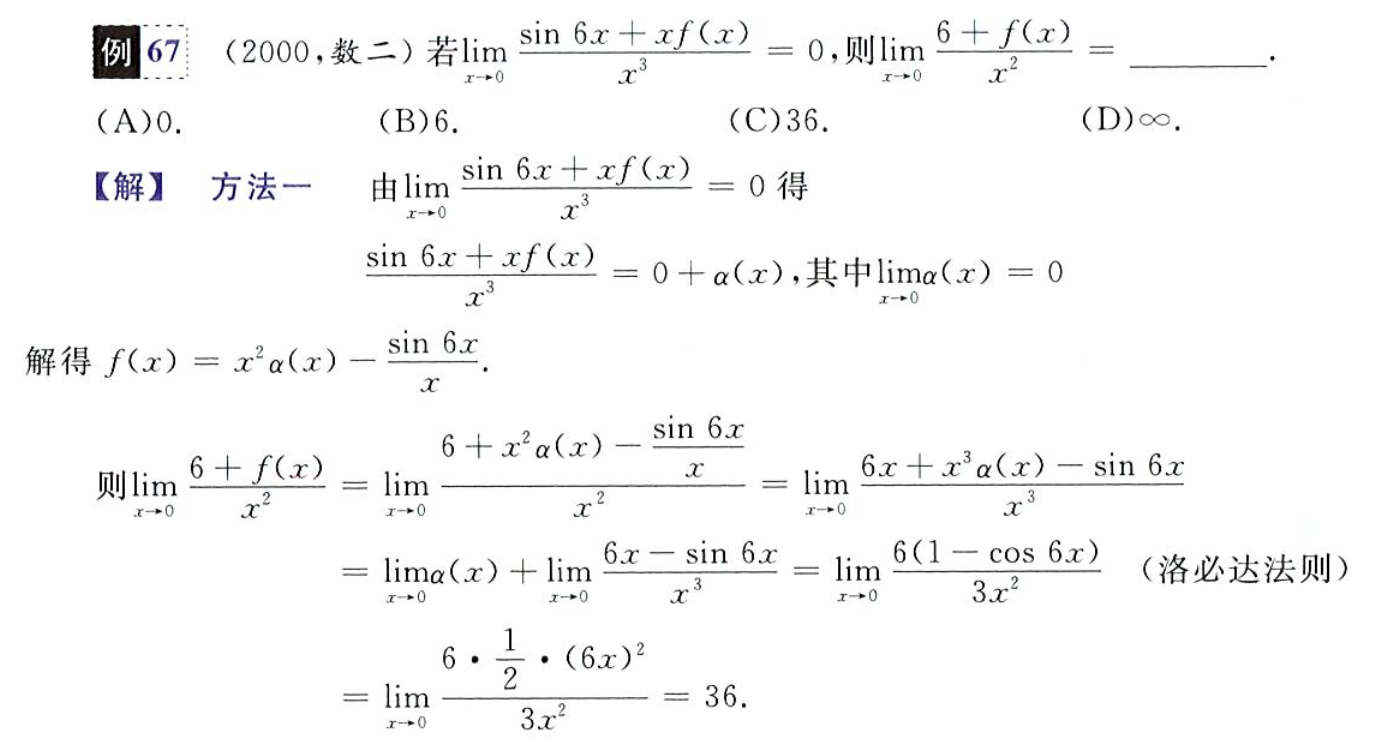
函数的连续性

连续性概念

连续原始定义

$$\lim_{\triangle x\rightarrow0}\triangle y = \lim_{\triangle x\rightarrow0}[f(x_0+\triangle x)-f(x_0)]=0$$

直观定义：极限等于函数值即为连续，左右都连续就连续

$$\lim_{\triangle x\rightarrow x_0}f(x) = \lim_{\triangle x\rightarrow x_0^-}f(x) = \lim_{\triangle x\rightarrow x_0^+}f(x) = f(x_0)$$

区间连续：函数在区间(a,b)内处处连续，则函数在区间(a.b)内连续

$$\lim_{x\rightarrow0}\,x^asin\frac{1}{x} = 0\,\,(a>0)$$

• 当 a <=0 时，该极限不存在

提供了一个新思路，多项式求极限时，能直接求得的项作为常数单独提出，处理不能直接求出的项（换元需要灵感）

连续函数运算

四则运算：若两个函数在同一点均连续，则他们的加减乘除均连续（但注意分母不能为 0）

复合函数的连续性：

$$\varphi(x)在x_0处连续且\varphi(x_0)=u_0\,\,,\,\, 同时f(u)在u_0处连续\\ 则f(\varphi(x))在x_0处连续$$

反函数的连续性：当原函数在区间内连续且单调，则其反函数在对应区间也连续且具有单调性（但相反）

初等函数连续性

初等函数连续性：初等函数在定义域内均连续

在定义域内其实就略去了函数不存在的情况，如tanx, 1/x，其在定义域中一定不存在Π/2和0

在讨论函数的连续区间时

• 着重处理断点：如分段函数的分段点，不存在的点
• 判断断点的连续性：分别计算左右极限，若不相等或不存在，确认在该点不连续
• 在讨论连续区间时，要把这个点去掉，不能包含

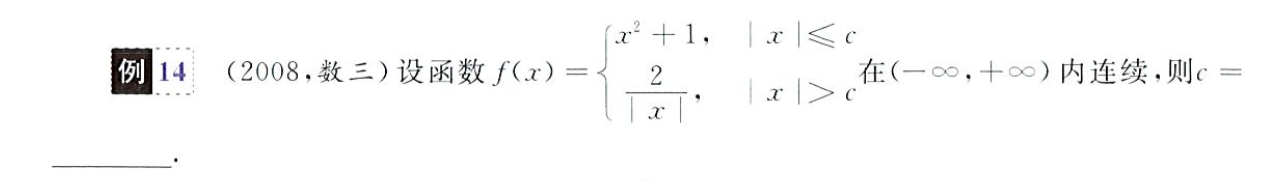
找出两个函数的交点，画图求解

不要想当然的令cosx (x->0)等于 1，其实是趋于 1

$$\lim_{x\rightarrow0}(cosx)^{1/x^2} = e^{-1/2}$$

间断点及其分类

x0 为 f(x) 的间断点 <=> f(x) 在 x0 点不连续

以下三个条件必有一个不成立

• f(x0) 有定义
• 当 x->x0，limf(x) 存在，
• x->x0，limf(x) = f(x0)

间断点的分类

• 第一类间断点：左右极限均存在
  • 可去间断点：左右极限相等
  • 跳跃间断点：左右极限不等
• 第二类间断点：左右极限至少有一个不存在
  • 无穷间断点：有至少一个极限趋于无穷
  • 震荡间断点：x->x0，limf(x) 震荡

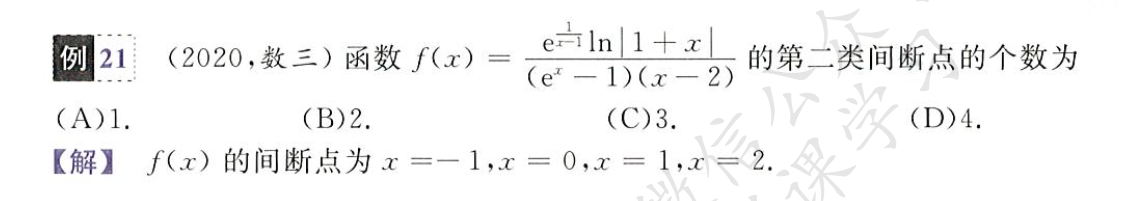
像这种判断间断点的题目的求极限很多都可以直接带，如果最后约不掉出现了分母为 0 或者分子无穷大的情况，直接判断其极限不存在（为无穷），属于第二类间断点

绝对值的处理必须慎重但简约，能晚则晚处理

一定要注意定义域的界限，很多时候判断间断点不仅仅是求极限，还有一些基本的问题；在处理分式时，一定要把分母为 0 和不为 0 的情况分开讨论并求极限

可去间断点和连续的区别：

这个地方x-arcsinx的处理，要么用洛必达洛几次，能洛出来

$$(arcsinx)' = \frac{1}{\sqrt{1-x^2}}$$

要么背一下泰勒展开（等价无穷小）

$$arcsinx-x \sim \frac{1}{6}x^3\,\,,\,\,x\rightarrow0$$

不要求极限求蠢了，看到 lim 就搁这疯狂代换，有的时候简单讨论一下就行

闭区间上连续函数的性质

最值定理：若函数在闭区间[a,b]内连续，必有最大值最小值

有界性定理：若函数在闭区间[a,b]内连续，必在区间内有界（最值定理推论）

介值定理：若函数在闭区间[a,b]内连续且f(a) != f(b)，对于min < cur < max，必存在c∈(a,b) 使得f(c) = cur

• 就是说一旦连续，从最小到最大的过程一定会有一个自变量对应函数值 C

零点定理：若函数在闭区间[a,b]内连续且f(a)f(b) < 0，必存在c使得f(c) = 0（介值定理推论）

求解闭区间上零点定理题目一般步骤：

• 根据等式建立函数
• 判断临界点函数值
  • 直接和 0 比较
  • 相乘比较是否小于 0
  • 若能等于 0，需要对结果分类讨论，如上题
• 根据零点定理（介值定理）得出结论

介值定理在使用时

• 假设区间内最大值 M 和最小值 m
• 对已给出的值进行和要求的值带入最大最小值建立不等式
• 将不等式两侧化为简单的 m 和 M 形式
• 根据介值定理带入 f(ξ)，对不等式移项一定可以得到要求的值

利用介值定理证明积分中值定理