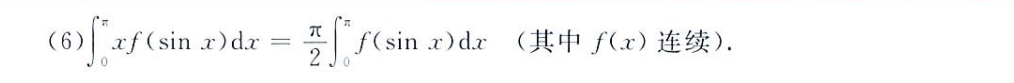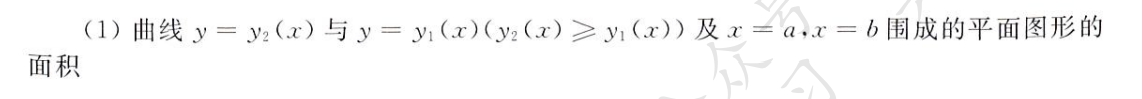一元函数积分学

不定积分与定积分概念性质

原函数、不定积分和定积分

主要涉及一个原函数到导函数的转换问题，也就是微分、积分、导数的转换

$$dy = y'dx \\ \int dy = \int y'dx = y+C \\ \int f(x)\,dx = \int dF(x) = F(x) + C$$

然后是定积分的连续性

$$\int_a^b f'(x)dx = \int_a^c f'(x)dx + \int_c^b f'(x)dx$$

通过导数大小，可以判断同区间内不同函数定积分的大小（定积分大小取决于高度差和跨度，同区间跨度相同，高度差取决于函数变化快慢，导数越大，原函数变化越快，自然高度差越大，定积分越大）

$$f'(x) \geq g'(x) \Rightarrow \int_a^b f'(x)dx \geq \int_a^b g'(x)dx$$

这里可以加入中间函数对不同导数进行一个判断，如在0-π/2之间判断sin(sinx) / cos(sinx)，可以明确的是在这一区间内，x > sinx（相减求最值）

• 因为sint在区间内递增，x和sinx作为自变量t，前者更大，由于递增，自然sin(sinx) < sinx
• 又因为cost在区间内递减，x和sinx作为自变量，前者更大，由于递减，所以cos(x) < cos(sinx)

我们分别求出sinx和cosx的定积分（基础积分），均为 1，则有sin(sinx) < 1 < cos(sinx) ，作为导数，后者在区间内始终大于前者，自然其定积分也更大，判断完毕

变限积分

一类很重要的定积分，其积分上或下界为自变量x的定积分，会积出一个原函数加减一个原函数值的形式，对这个定积分重新求导会得到原导函数

$$\int_a^xf(t)dt = F(x)-F(a)\\ [F(x)-F(a)]' = f(x)$$

积分中值定理

$$\exist\,\xi \in (a,b) \,使得\, f(\xi) = \frac{\int_a^bf(x)dx}{b-a}$$

即：在区间(a,b)内始终存在一点函数值等于其函数均值

不定积分与定积分计算

基本积分公式

基本积分方法

换元法

第一类换元法（凑微分法）：将 d 左边的项积分化到 d 右边，并将其试做一个整体 u 对剩下部分进行积分

第二类换元法（换元积分法）：将 d 右边的项，如 x 化为 log t，同样的要将 d 左边的 x 进行替换，然后将 log t 微分，d 右边仅保留 t（即 dt，对 t 进行积分）

常见几种典型类型的换元法

万能代换

$$令\,tan\frac{x}{2} = t \Rightarrow sinx = \frac{t}{1+t^2}\,\,,\,\, cosx = \frac{1-t^2}{1+t^2}\\ dx = 2d(arctant) = \frac{2}{1+t^2}dt$$

定积分的换元积分：就是第二类换元法 ＋ 第一类换元法 ＋ 牛顿莱布利兹公式求解定积分

牛顿莱布利兹公式

$$\int _a^bf(x)dx = F(a)-F(b)$$

分部积分法

$$\int u(x)dv(x) = u(x)v(x) - \int v(x)du(x)$$

几个好用的定积分公式

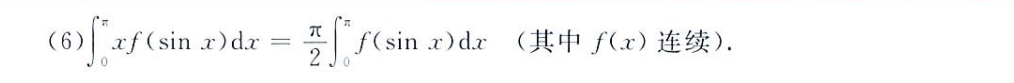
反常积分及其计算

反常积分

对于定积分，若上下界至少有一个为无穷，则称该积分为无穷区间上的反常积分

• 若自变量趋于无穷时，被积函数极限值存在，则称该反常积分收敛
• 若极限值不存在，即被积函数函数值趋于无穷，则称其发散

瑕积分：对于被积函数f(x)若其在x=a处发散（即函数值趋于无穷），对该函数进行定积分时上下界包含了 a 点，则该积分为瑕积分，也是一种反常积分

• 当lim f(a) = 无穷时，该瑕积分发散；若为常数，则收敛
• 点 a 也被称作瑕积分 f(x) 的奇点

对称区间上奇偶函数的反常积分

一定要注意这里奇偶函数反常积分的规律都是建立在收敛的基础上，一旦发散，各种规律将不存在，一定要先判断反常积分的收敛性

一个误解：对于偶函数f(x)，F(+∞) - F(-∞) != 0，一定不能有这种幻觉，这显然是不对的，因为+∞ + 1 = +∞，你无法对其划等号

$$\int _{-∞}^{+∞} 2xdx = x^2 |_{-∞}^{+∞} = 0$$

一个重要的反常积分

$$\int_{-∞}^{+∞} e^{-x^2} = \sqrt{\pi}$$

定积分的应用

物理题

基本方法

就是微分法：要求某个量的积量（积分），如w，首先找他的微分，即dw，然后在给定区间上对dw进行积分求值，即为微分法

重要几何公式和物理应用

平面图形面积

极坐标系下，自变量为角度，因变量为线段长度

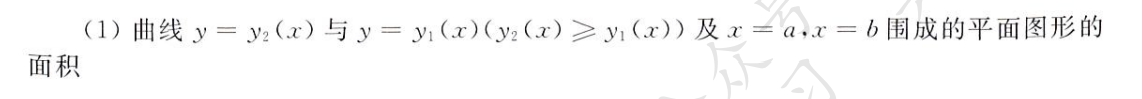
旋转体体积

函数的平均值

将函数在区间内视作一个长方形，长为区间长度，平均值即为其平均宽度

$$f_均 = \frac{\int_a^bf(x)dx}{b-a}$$

已知横截面积求体积

就是对截面积分，求得体积

$$V = \int_a^bS(x)dx$$

平面曲线的弧长

已知弧长公式，就是加了一个定积分，注意极坐标系下的公式

旋转曲面面积

和旋转曲面体积完全不同，一个是面积，一个是体积

相较于旋转曲面体积，明显不同捏

$$V = \pi\int_a^by(x)^2dx$$

在求绕 y 轴旋转的曲面面积时，实际上是在对圆周长进行积分，所以用到了 2π，和这里还是有点点像

$$V = 2\pi\int_a^b xy(x)dx$$

其他物理应用：变力做功；液体静压力；引力；物体的质心（球心）

再说，要深刻理解微分法思想

定积分的综合题

结合函数性质（单调性、奇偶性）、极限、夹逼定理、中值定理考察不定积分、定积分、反常积分、变限积分，一整个大锅汇

考察定积分的奇偶性

结合夹逼定理考察定积分

结合中值定理和单调性考察定积分应用