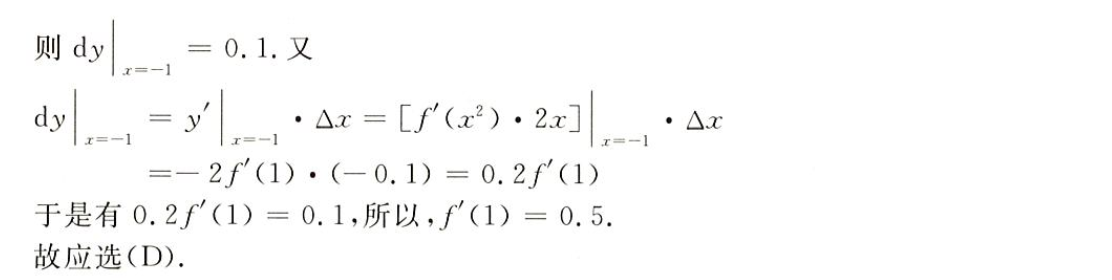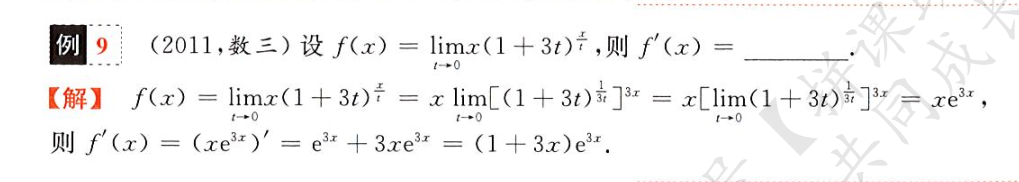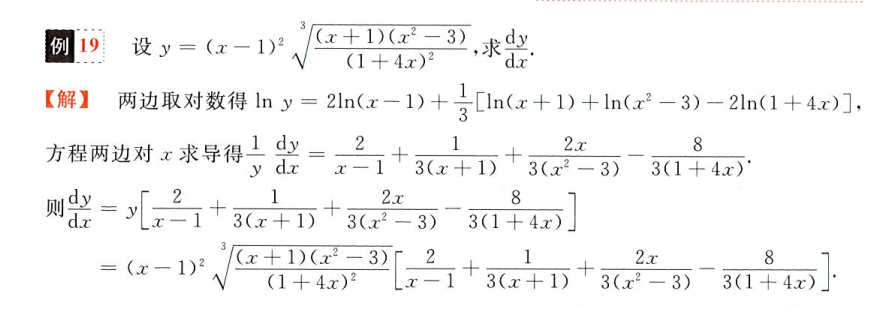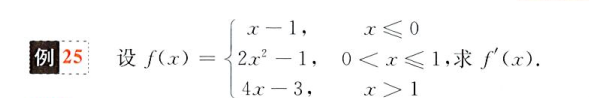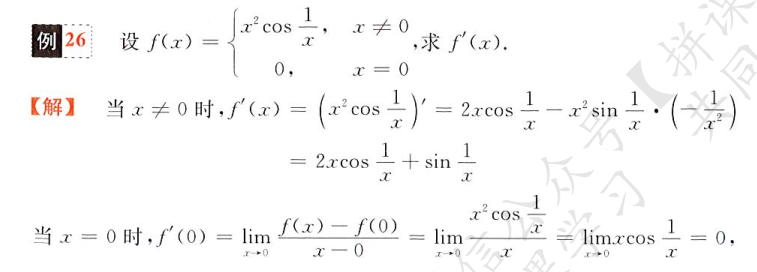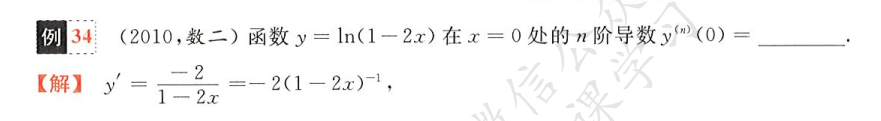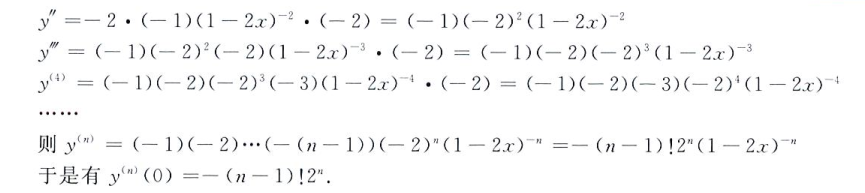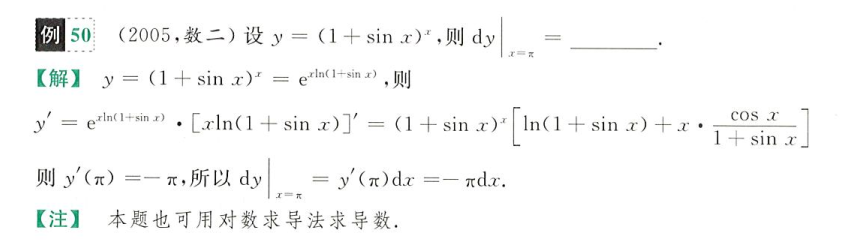一元函数微分学

导数和微分概念

导数的概念及几何意义

导数概念

导数概念：若f(x0)有定义，则函数f在x0的导数为

$$f(x_0)' = \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x} = \lim_{\triangle x\rightarrow0}\frac{f(x_0+\triangle x) - f(x_0)}{\triangle x}$$

左导数和右导数：求极限的时候取正反，右极限对应右导数，左极限对应左导数，记作

$$f'_{-}(x_0)\,,\,f'_{+}(x_0)$$

可导

• 函数在某处可导：函数在该处左右导数均存在且相等（充要）
• 函数区间可导：函数在区间内任意一点均可导

对于求单点的导数，多采用定义求解

• 根据定义求导数，如
  $$求\,f(x)\,在\,x=1\,的导数\\ 则求\,\lim_{x\rightarrow0}\frac{f(1+x)-f(1)}{x}$$
  左导数则x->0-，右导数则x->0+，等价于
  $$\lim_{x\rightarrow1}\frac{f(x)-f(1)}{x-1}$$

• 不需要看到绝对值就一定分情况讨论，直接不化绝对值求解，最后一步化开绝对值可能简便无数倍

• 分割极限式，分别计算再相乘
• 这里定义求导数令x->0 -/+也可，我倾向于设变化的 x 趋于 0 来求极限

已知函数在 x0 连续，基于此进行一些个代换

$$\lim_{\triangle x\rightarrow0}\frac{f(x_0+\triangle ax)-f(x_0)}{\triangle x} = af'(x_0)$$

• 分母也乘以 a 后等于f'(x0)，所以原式为 a 倍的f'(x0)

凑分母 - 自变量，纯尼玛流氓解法

一定要明确下面两种定义，力求令函数括号内等于分母，进行这一个从极限到导数的替换，但要时刻注意需满足这里趋近条件

$$\mathop{lim}_{🐕\rightarrow x_0}\frac{f(🐕)-f(x_0)}{🐕-x_0}\\ \mathop{lim}_{🐕\rightarrow 0}\frac{f(x_0+🐕)-f(x_0)}{🐕}\\$$

导数几何意义

导数即为切线斜率

切线方程

$$y-f(x_0) = f'(x_0)(x-x_0)$$

法线：和切线垂直，斜率为导数的倒数的负数

$$y-f(x_0) = \frac{-1}{f'(x_0)}(x-x_0)$$

注意若导数为 ∞ 但函数连续，说明该点的切线为一条平行于 x 轴的直线

结合导数的定义考察，无非在求导的基础上加了一条直线定义

微分的概念及几何意义

微分概念

微分，即微小的变化量

先考虑因变量 y 在自变量 x 微小变化时的变化量 ▲y

$$\triangle y = f(x_0+\triangle x)-f(x_0)$$

若上式可以表示为这样的多项式形式，则称该函数在x0点可微

$$\triangle y = A\triangle x + o(\triangle x)$$

• 其中 A 为一个表达式（多项式）
• o(x) 为 ▲x 的高阶无穷小，即当 x 趋于 0 时该项被视为 0

理所当然的，当 x 微小变化时，y 的变化仅由Ax决定，于是我们定义微分

$$dy = A\triangle x$$

在实际函数中，这个 A 就是导数，x 即为 dx

$$dy = f'(x_0)\triangle x = f'(x_0)dx$$

• 这个d有取无穷小的意思，如dx表示x, x->0，也就是所谓微分

给我狠狠地代入定义

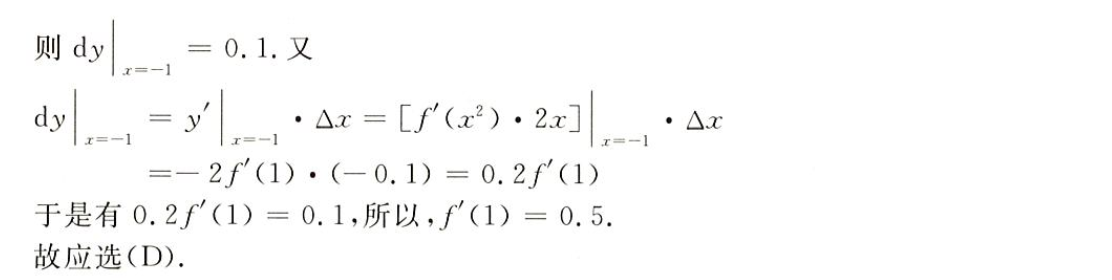
注意，这两种写法是完全等价的

$$\mathop{lim}_{\triangle x\rightarrow0}\triangle x\sim dx$$

微分几何意义

微分的几何意义：就是当自变量微小变化时，纵坐标的增量

但要注意增量总是大于微分，除了当自变量趋于 0 时

连续、可导、可微的关系

可导是可微的充分必要条件，连续不一定可导，可导一定连续

• 连续是函数值极限相等
• 可导是函数值变化量极限相等

其实也没有这么麻烦，从直觉上来说，如果f(x)在x=0处可导，也就是说下式存在

• 已经假设可导，所以连续，故f(0) = limf(x) = 0

$$\lim_{\triangle x\rightarrow0}\frac{f(\triangle x)}{\triangle x}$$

换一个说法，f(x)和x是同阶无穷小，于是可以直接根据无穷小的阶数判断选项是趋于 0 还是无穷

这里一定要注意在分子分母都趋于 0 时，分母阶数越高，整体将趋于无穷，不要想当然的觉得更高阶就会趋于 0，越高表示越小

导数和微分的计算

导数的计算

初等函数求导公式

实际上就是泰勒展开的第一项

复合函数求导

$$[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)\\ ---------------\\ [\frac{f(x)}{g(x)}]' = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\\ ---------------\\ f[g(x)]' = f'(u)g'(x)\,,\,\,u = g(x)$$

对复杂函数求导，尽量先化简，特别对于对数中套指数，将指数作为系数提出，对数乘除化为对数加减，同底指数乘除化为指数加减

带有极限的函数求导，把 x 视作常数，运用第二个重要极限化简

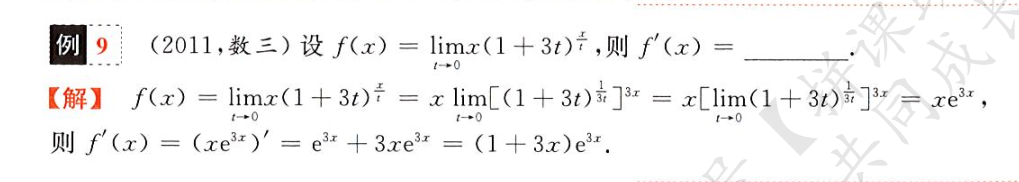
复合函数求导

复合函数求导，严格遵守展开规律

反函数求导

反函数：将自变量和因变量的关系置换，但不改变原函数等式，如y = arccosx的反函数为x = cosy，y = arctanx的反函数为x = tany

反函数求导法则，设f(x)为原函数g(y)为其反函数，则

$$f(x)' = 1/g(y)'$$

如

$$arcsinx' = \frac{1}{sixy'} = \frac{1}{cosy} = \frac{1}{(1-sin^2y)^{1/2}} = \frac{1}{(1-x^2)^{1/2}}$$

重点在于反函数为x = siny，且该等式可以把 y 代换为 x

隐函数求导

所谓隐函数，就是在函数表达式中，隐藏了一个以 x 为自变量的函数，这个函数可以是其自身，如tany = ln(x+y)+2x，在这要求其导数y'，则要对等式两侧同时对 x 求导，得

$$(1+y^2)y' = \frac{y'}{x+y}+2 \Rightarrow y' = \frac{2}{1+y^2-\frac{1}{x+y}}$$

结合导数定义考察

$$f(x)' = \lim_{\triangle x\rightarrow0}\frac{f(x+\triangle x)-f(x)}{\triangle x}$$

对数求导法

对于形如

$$y = f(x)^{g(x)}$$

的函数，对等式两侧加上对数ln

$$lny = ln\,f(x)^{g(x)}$$

再分别求导，移项得到y'，即dy/dx

也可以像求指数极限那样，化为

$$y = e^{g(x)lnf(x)}$$

再对该等式求导得到y'

要注意的是，最后得到y'后，要把y换成x的表达式（因为lny求导必得y'/y存在一个y，移项后再代换）

举个栗子

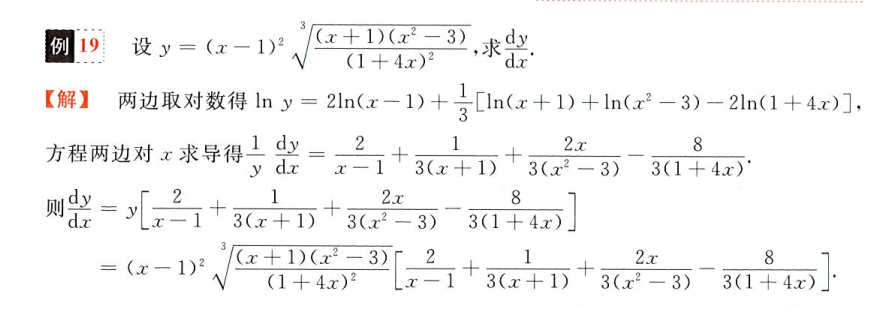
化简属于基本功

参数方程求导

给定y和x关于t的函数式，则

$$y' = \frac{dy}{dx} = \frac{dy/dt}{dx/dt}$$

举个栗子

分段函数求导

就是一段段求，但是要注意判断一个分段点是否存在导数

• 导数是否存在，根据定义，即左右极限是否相同

像这个函数，他的分段点x=0很明显左右极限不同，左极限为 1，右极限为 0，所以f'(x)在x=0处没有定义，在写时要剔除掉该点

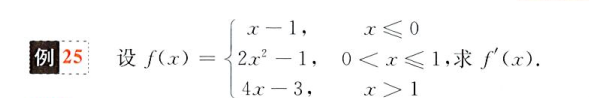
有时要根据定义求断点极限，举个栗子

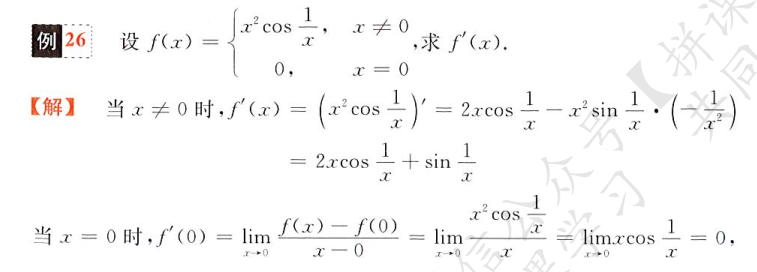
有关导数的重要结论

偶函数导数为奇函数

奇函数导数为偶函数

周期函数导数为周期函数，且周期不变

高阶导数的计算

找规律

普通复合函数直接导就行，进行一个规律的找

这里用到奇偶性：奇函数导数为偶，偶函数导数为奇，无限循环

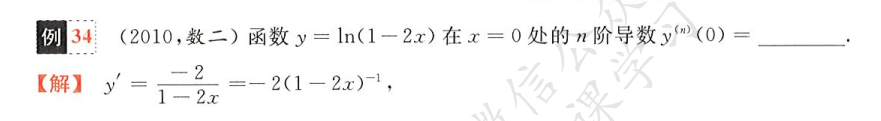
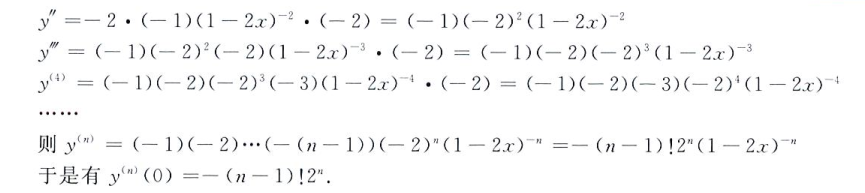
纯纯的找规律，指数求高阶导会出现阶乘，指数为负要考虑 n 时的正负号

莱布利茨公式

对于某些没有明显规律的复合函数求高阶，可能要用到莱布里茨公式

$$[f(x)g(x)]^n = \sum_{i=0}^{n}\,C_n^i\,f(x)^i\,g(x)^{n-i}$$

三角变换

注意有些三角函数的变换，在求导时，最好化为同一三角函数（如全化为 sin）进行一个规律的找

特殊二阶导

抽象复合函数的二阶导，直接求就完事了，直接用f'(x)和f''(x)写

由方程确定的隐函数的二阶导

• 先算一阶导，用 x 和 y 表示
• 再对一阶导求导，得到二阶导，同样要全部用 x 和 y 表示

在第二部中肯定还会出现一阶导，即 y'，一定要把最后结果里的 y' 用第一步求出来的式子代入并化简

参数方程的二阶导

$$y' = \frac{dy/dt}{dx/dt}\Rightarrow y'' = \frac{dy'/dt}{dx/dt}$$

这个 y' 实际上求出来也是一个关于 t 的函数，要求他关于 x 的导数（也就是 y 的二阶导），就是对这个关于 t 的函数再对 x 求一次导，可能有点绕，所以这里求二阶导的分母仍然是dx/dt

微分的计算

就是在求导数的基础上加上一个dx，即正常求导，再在导数后乘上一项dx

$$y' = \frac{dy}{dx} \Rightarrow dy = y'dx$$

当然可以直接对dy进行微分，其实是一样的

$$df(x) = f'(x)dx$$

你譬如

$$dy = dx^2 = 2xdx$$

举个栗子

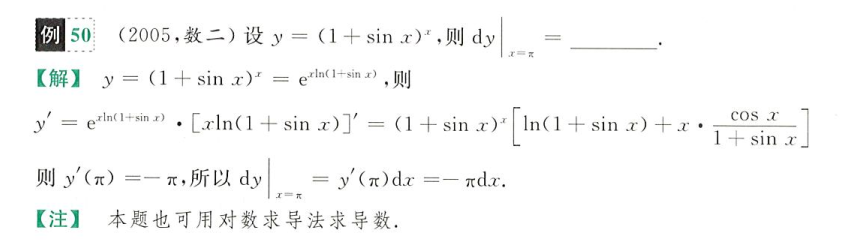
当然我习惯的求法是这样，令

$$lny = xln(1+sinx)$$

在对方程两边对x求导，移项解出y'，将y用原式替代（不替也行，因为这里是求具体值），最后带入x=Π求解

中值定理、不等式与零点问题

中值定理

费马定理

极值点的导数一定为 0

罗尔定理

两个相等的函数值之间，必有一点导数为 0

拉格朗日中值定理

连续可导函数的两点之间必有某点的斜率等于该区间的平均斜率

$$\frac{f(x)-f(x_0)}{x-x_0} = f'(\xi)\\ -----------\\ f(x) = f(x_0) + (x-x_0)f'(\xi)$$

其中

$$\xi \in [x_0, x]$$

柯西中值定理

可以视作拉氏定理的推广：在参数方程形式下的拉格朗日中值定理

相应的，拉氏定理可以视作柯西中值定理的特殊情况：即g(x)=x时的柯西中值定理

$$\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(\xi)}{g'(\xi)}$$

柯西中值定理的罗尔定理证明，设F(X)

$$F(x) = [f(b)-f(a)]\,[g(x)-g(a)] - [g(b)-g(a)]\,[f(x)-f(a)]$$

当x=a/b时，代入F(x)可知F(a) = F(b) = 0，根据罗尔定理，必有

$$\xi \in [a,b]\,\,令\,\,F'(\xi) = 0$$

又可知

$$F'(x) = [f(b)-f(a)]\,g(x) - [g(b)-g(a)]\,f(x)$$

将ξ代入F'(x)，可得

$$0 = [f(b)-f(a)]\,g(\xi) - [g(b)-g(a)]\,f(\xi)$$

移项得

$$\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(\xi)}{g'(\xi)}$$

即为柯西中值定理

泰勒公式

基本思想：以多项式逼近光滑曲线，用开口不同的奇偶函数相加以逼近曲线

• 奇偶函数即指（其中o(x^n)表示x^n的无穷小项）

  $$a_1x + a_2x^2 + a_3x^3 + ... + a_nx^n + o(x^n)$$

• 其系数由导数反向确定

泰勒展开式

$$f(x) = f(x_0) + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + ... + \frac{f^n(x_0)}{n!}(x-x_0)^n + R_n(x)$$

x 的指数越来越高，是因为越逼近差距越小，于是相加的项数越来越趋近无穷小以实现逼近的效果

注意，当x0 = 0时，泰勒公式退化成麦克劳林公式

拉格朗日余项和佩亚诺余项

拉格朗日余项：泰勒多展一轮，自变量ξ为x-x0之间的某一常数

$$R_n(x) = \frac{f^{n+1}(\xi)}{(n+1)!}(x-x_0)^{n+1}$$

佩亚诺余项：即为x^n的高阶无穷小

$$R_n(x) = o((x-x_0)^{n})$$

就是高阶无穷小的两种表达方式

常见的佩亚诺余项的麦克劳林展开

用泰勒展开解决无穷小问题：这里不需要考虑等价无穷小必须是乘除才能替换的问题，泰勒展开是严格的等价，直接替换

这个吊展开直接看不懂，但有理化的方法值得借鉴

不等式的证明

证明不等式

• 单调性
• 最值
• 拉格朗日中值定理：证明关于斜率的不等式
• 泰勒展开的拉格朗日余项：通过移动展开位置，一到两次展开转换原式子（用泰勒展开等价替代），对不等式进行转换

零点问题

连续函数介值定理

罗尔定理

• 一般来说，都是通过导数对于原函数的趋势进行一定的限制，原函数对导数的趋势没有必然影响

结合导数判断原函数极值 / 最值对零点进行判断

导数应用

极值

包括驻点、拐点、弧微分、曲率-曲率-曲率半径-曲率中心问题

驻点：一阶导为 0 的点，意为驻留；当碰到不可导的点时（不连续），通过定义进行判断，即驻点的邻域内驻点对应函数值为最小 / 最大

拐点：二阶导为 0 的点；和驻点同理，当二阶导在该点两侧异号时（该点不连续），凹凸性改变，同样为拐点

弧微分：即曲线微分，在变化量很小时等于三角形的斜边

$$ds = \sqrt{(dx)^2 + (dy)^2} = \sqrt{1+y'^2}dx$$

曲率：表示角度随弧变化的速度

$$tan\theta = dy/dx \Rightarrow \theta = arctan\,dy/dx\\ d\theta = d\,arctan \frac{dy}{dx} \Rightarrow \frac{d\theta}{ds} = \frac{d\,arctan\frac{dy}{dx}}{ds}$$

求导约去dx可得

$$K = d\theta = \frac{y''}{(1+y'^2)^{3/2}}$$

曲率半径即为1/K，曲率中心即为在当前点的发线上距离该点1/K的点（弧内侧）

最值

需要考虑不可导点、极值点、自变量边界

凹凸

考虑二阶导数正负，正为凹，负为凸（从上往下看）

渐进

水平渐进线：自变量取无穷时，因变量为常数，则为水平渐进线

垂直渐进线：自变量取常数，因变量为无穷，则为垂直渐进线

斜渐进线：自变量取常数，f(x)/x在该点极限为常数，则存在斜渐进线，斜率为lim f(x)/x，过点(x,f(x))