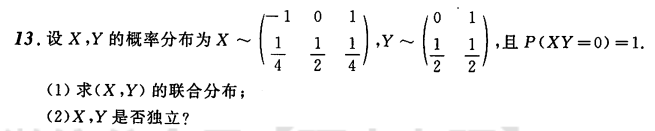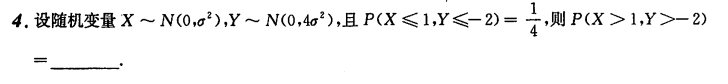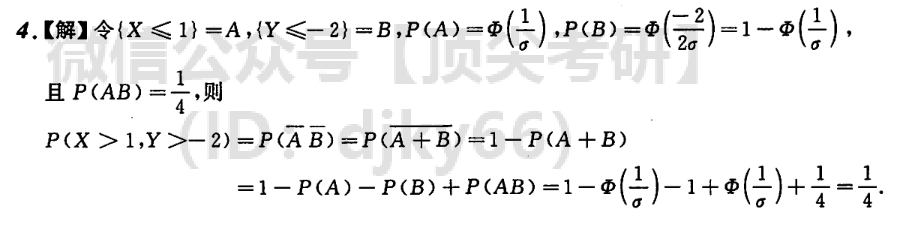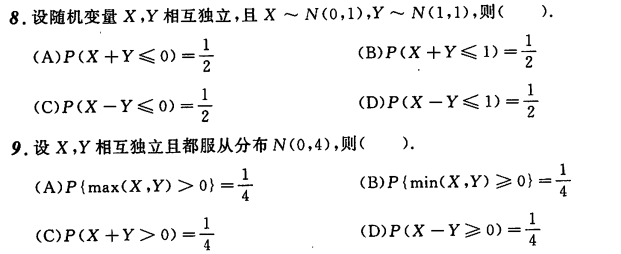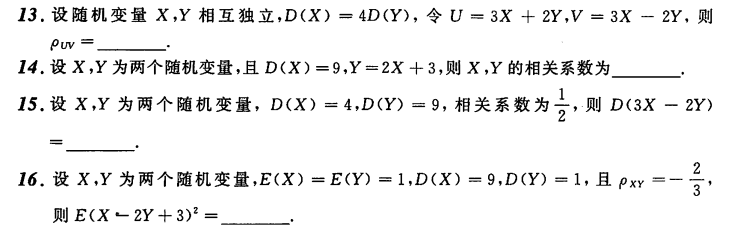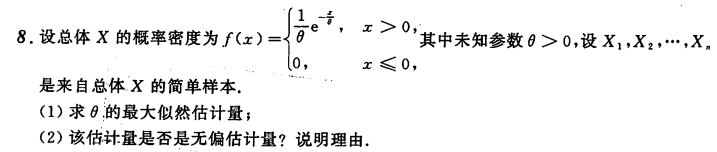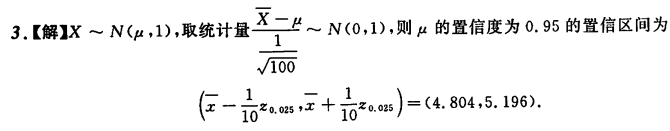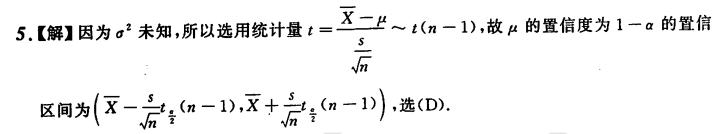随机事件和概率 不相容和独立的区别,不相容指二者不能同时发送
P ( A B ) = 0
P(AB) = 0
P ( A B ) = 0 P ( A ∣ B ) = P ( A ) P ( A B ) = P ( A ) P ( B )
P(A|B) = P(A) \quad P(AB) = P(A)P(B)
P ( A ∣ B ) = P ( A ) P ( A B ) = P ( A ) P ( B )
对于 17 题,显而易见,条件概率满足
P ( A ‾ ∣ B ‾ ) = P ( A ‾ ∣ B )
P(\overline{A}|\overline{B}) = P(\overline{A}|B)
P ( A ∣ B ) = P ( A ∣ B ) P ( A ‾ ∣ B ‾ ) = 1 − P ( A ∣ B ) = P ( A ‾ ∣ B )
P(\overline{A}|\overline{B}) = 1-P(A|B) = P(\overline{A}|B)
P ( A ∣ B ) = 1 − P ( A ∣ B ) = P ( A ∣ B ) 1 = P ( A ∣ B ) + P ( A ‾ ∣ B )
1 = P(A|B) + P(\overline{A}|B)
1 = P ( A ∣ B ) + P ( A ∣ B )
条件概率问题
一维随机变量 密度函数和分布函数转换 当已知密度函数 f 求分布函数时,需要注意
对于分布函数 F 一定要表明 0 和 1 的部分,定义域应包含整个实数域 另外在积分的时候,一定是求定积分,上下限一定要明确,直接求不定积分再手动加限是不对的 常见分布表示和密度函数 常见分布的符号表示
连续型 离散型 正态分布 N(μ, ν) 二项分布 B(n, p) 均匀分布 U(a, b) 0/1 分布 B(1, p) 指数分布 E(λ) 泊松分布 P(λ) 几何分布 GE(p)
指数分布密度函数和分布函数为
f ( x ) = λ e − λ x F ( x ) = 1 − e − λ x
f(x) = \lambda e^{-\lambda x} \quad F(x) = 1-e^{-\lambda x}
f ( x ) = λ e − λ x F ( x ) = 1 − e − λ x 1/(b-a)
泊松分布的分布函数
P ( x ) = λ x x ! e − λ
P(x) = \frac{\lambda^x}{x!}e^{-\lambda}
P ( x ) = x ! λ x e − λ
设不成功概率为 q = 1-p,则
P ( X = k ) = q k − 1 p
P(X=k) = q^{k-1}p
P ( X = k ) = q k − 1 p
几何分布的方差
D ( X ) = 1 − p p 2
D(X) = \frac{1-p}{p^2}
D ( X ) = p 2 1 − p
一维正态分布 一维正态分布
X ∼ N ( μ , υ ) → p ( x ) = 1 2 π υ e − ( x − μ ) 2 2 υ
X\sim N(\mu,\upsilon) \rightarrow p(x) = \frac{1}{\sqrt{2\pi}\,\upsilon}e^{-\frac{(x-\mu)^2}{2\upsilon}}
X ∼ N ( μ , υ ) → p ( x ) = 2 π υ 1 e − 2 υ ( x − μ ) 2
三道有关一维正态的性质栗题
二维随机变量 二维离散随机变量 在这种二维离散分布的耦合中,显然 X1 和 X2 是不独立的,二者组合为二维离散分布后出现了条件限制,并非各自概率直接相乘
不能说一模一样,只能说极其相似
二维正态分布 不太懂
选择 D、B,根据对称性很容易得出答案
多维随机变量函数 重难点
一维到多维的转换:从分布函数的定义入手,二重积分,找上下限是关键
T17、20、23、27
条件概率密度 二维随机变量的条件概率密度公式
f X ∣ Y ( x ∣ y ) = f ( x , y ) f Y ( y )
f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)}
f X ∣ Y ( x ∣ y ) = f Y ( y ) f ( x , y )
多维随机变量的独立性 独立性的判断,当二维随机变量边际密度函数满足
p X ( x ) p Y ( y ) = p ( x , y )
p_X(x)p_Y(y)=p(x,y)
p X ( x ) p Y ( y ) = p ( x , y )
试算法判断独立性,如对于均匀分布 X~U(0,2),随机变量 Y = X^2,则
P ( X < 1 , Y < 1 ) = P ( X < 1 ) = 1 2
P(X<1,Y<1) = P(X<1) = \frac{1}{2}
P ( X < 1 , Y < 1 ) = P ( X < 1 ) = 2 1 P ( X < 1 ) P ( Y < 1 ) = 1 2 × 1 2 = 1 4
P(X<1)P(Y<1) = \frac{1}{2}\times\frac{1}{2}= \frac{1}{4}
P ( X < 1 ) P ( Y < 1 ) = 2 1 × 2 1 = 4 1
随机变量的数字特征 常见分布的期望和方差 同一随机变量的期望和方差满足
D ( X ) = E ( X 2 ) − [ E ( X ) ] 2
D(X) = E(X^2)-[E(X)]^2
D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 E ( 2 X + 1 ) = 2 E ( X ) + E ( 1 ) D ( 2 X + 4 ) = 2 2 D ( X )
E(2X+1) = 2E(X)+E(1)\quad D(2X+4) = 2^2D(X)
E ( 2 X + 1 ) = 2 E ( X ) + E ( 1 ) D ( 2 X + 4 ) = 2 2 D ( X )
指数分布
f ( x ) = λ e − λ x → E ( X ) = 1 λ D ( X ) = 1 λ 2
f(x) = \lambda e^{-\lambda x} \rightarrow E(X) = \frac{1}{\lambda}\quad D(X) = \frac{1}{\lambda^2}
f ( x ) = λ e − λ x → E ( X ) = λ 1 D ( X ) = λ 2 1 E ( x ) = ∫ a b x d x b − a E ( x 2 ) = ∫ a b x 2 d x b − a
E(x)=\int_a^b\frac{xdx}{b-a}\quad E(x^2)=\int_a^b\frac{x^2dx}{b-a}
E ( x ) = ∫ a b b − a x d x E ( x 2 ) = ∫ a b b − a x 2 d x E ( X ) = a + b 2 D ( X ) = b 2 − a 2 12
E(X) = \frac{a+b}{2}\quad D(X) = \frac{b^2-a^2}{12}
E ( X ) = 2 a + b D ( X ) = 12 b 2 − a 2 X ∼ N ( u , v 2 ) ⇒ f ( x ) = 1 2 π v e − ( x − u ) 2 2 v → E ( X ) = u D ( X ) = v 2
X\sim N(u,v^2)\Rightarrow f(x)=\frac{1}{\sqrt{2\pi}v}e^{-\frac{(x-u)^2}{2v}}\rightarrow E(X)=u\quad D(X)=v^2
X ∼ N ( u , v 2 ) ⇒ f ( x ) = 2 π v 1 e − 2 v ( x − u ) 2 → E ( X ) = u D ( X ) = v 2
方差、协方差和相关系数 方差的运算
D ( X + Y ) = D ( X ) + D ( Y ) + 2 ρ D ( X ) D ( Y )
D(X+Y) = D(X)+D(Y)+2\rho\sqrt{D(X)D(Y)}
D ( X + Y ) = D ( X ) + D ( Y ) + 2 ρ D ( X ) D ( Y ) 2 ρ D ( X ) D ( Y ) 等价于 2 C o v ( X , Y )
2\rho\sqrt{D(X)D(Y)}\quad 等价于\quad 2Cov(X,Y)
2 ρ D ( X ) D ( Y ) 等价于 2 C o v ( X , Y ) C o v ( U , V ) = E ( U V ) − E ( U ) E ( V )
Cov(U,V) = E(UV) - E(U)E(V)
C o v ( U , V ) = E ( U V ) − E ( U ) E ( V ) ρ = C o v ( U , V ) D ( U ) D ( V )
\rho = \frac{Cov(U,V)}{\sqrt{D(U)D(V)}}
ρ = D ( U ) D ( V ) C o v ( U , V ) C o v ( X , X ) = E ( X 2 ) − E 2 ( X ) = D ( X ) ρ = 1
Cov(X,X) = E(X^2)-E^2(X) = D(X) \quad \rho = 1
C o v ( X , X ) = E ( X 2 ) − E 2 ( X ) = D ( X ) ρ = 1 C o v ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) = 0
Cov(X,Y) = E(XY)-E(X)E(Y) = 0
C o v ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) = 0 C o v ( X , C ) = E ( X C ) − E ( X ) E ( C ) = C E ( X ) − C E ( X ) = 0
Cov(X, C) = E(XC)-E(X)E(C) = CE(X)-CE(X) = 0
C o v ( X , C ) = E ( XC ) − E ( X ) E ( C ) = CE ( X ) − CE ( X ) = 0 C o v ( X , Y ) = E ( 2 X 2 + X ) − E ( X ) E ( 2 X + 1 )
Cov(X,Y) = E(2X^2+X)-E(X)E(2X+1)
C o v ( X , Y ) = E ( 2 X 2 + X ) − E ( X ) E ( 2 X + 1 ) 2 E ( X 2 ) + E ( X ) − E ( X ) [ 2 E ( X ) + 1 ] = 2 E ( X 2 ) − 2 E 2 ( X ) = 2 D ( X )
2E(X^2)+E(X)-E(X)[2E(X)+1] = 2E(X^2)-2E^2(X) = 2D(X)
2 E ( X 2 ) + E ( X ) − E ( X ) [ 2 E ( X ) + 1 ] = 2 E ( X 2 ) − 2 E 2 ( X ) = 2 D ( X ) D ( X ) D ( Y ) = D ( X ) D ( 2 X + 1 ) = 4 D 2 ( X ) = 2 D ( X )
\sqrt{D(X)D(Y)} = \sqrt{D(X)D(2X+1)} = \sqrt{4D^2(X)} = 2D(X)
D ( X ) D ( Y ) = D ( X ) D ( 2 X + 1 ) = 4 D 2 ( X ) = 2 D ( X )
协方差的分配律
C o v ( X + 2 Y , X − 2 Y )
Cov(X+2Y,X-2Y)
C o v ( X + 2 Y , X − 2 Y ) C o v ( X , X ) + C o v ( X , − 2 Y ) + C o v ( 2 Y , X ) + C o v ( 2 Y , − 2 Y )
Cov(X,X)+Cov(X,-2Y)+Cov(2Y,X)+Cov(2Y,-2Y)
C o v ( X , X ) + C o v ( X , − 2 Y ) + C o v ( 2 Y , X ) + C o v ( 2 Y , − 2 Y ) 单个 变量以期望的形式参与运算(期望的系数提出均为线性,方差为平方),进一步为(中间项约掉)
C o v ( X , X ) − 4 C o v ( Y , Y )
Cov(X,X)-4Cov(Y,Y)
C o v ( X , X ) − 4 C o v ( Y , Y )
一些相互转化的栗题,掌握上述规律绝对可以秒杀
不相关和独立 不相关即指,两随机变量相关系数 ρ = 0,满足
C o v ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) = 0
Cov(X,Y) = E(XY)-E(X)E(Y) = 0
C o v ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) = 0 E ( X Y ) = E ( X ) E ( Y )
E(XY) = E(X)E(Y)
E ( X Y ) = E ( X ) E ( Y ) P ( X Y ) = P ( X ) P ( Y )
P(XY) = P(X)P(Y)
P ( X Y ) = P ( X ) P ( Y )
独立和不相关的内在含义是什么???
大数定律 切比雪夫不等式 切比雪夫
P { ∣ X − E ( X ) ≥ x ∣ } = D ( X ) x 2
P\{|X-E(X) \geq x|\} = \frac{D(X)}{x^2}
P { ∣ X − E ( X ) ≥ x ∣ } = x 2 D ( X ) P { ∣ X − E ( X ) ≤ x ∣ } = 1 − D ( X ) x 2
P\{|X-E(X) \leq x|\} = 1-\frac{D(X)}{x^2}
P { ∣ X − E ( X ) ≤ x ∣ } = 1 − x 2 D ( X )
大数定律 所有的大数定律好像都基于切比雪夫不等式
多随机变量大数定律:对于随机变量们x1,x2,...,xn,他们满足同一分布且具有相同的期望与方差(有时表述为x1,x2,...,xn为来自同一总体的简单随机样本),那么设这堆随机变量的均值为
X ‾ = 1 n ∑ i = 1 n X i
\overline{X} = \frac{1}{n}\sum_{i=1}^nX_i
X = n 1 i = 1 ∑ n X i P { ∣ X ‾ − E ( X ) ∣ ≥ x } = D ( X ) n x 2
P\{|\overline{X}-E(X)| \geq x\} = \frac{D(X)}{nx^2}
P { ∣ X − E ( X ) ∣ ≥ x } = n x 2 D ( X )
二项分布的收敛 二项分布收敛于正态分布
当随机变量 X 满足二项分布 X~B(n, p),则有
P { X − E ( X ) D ( X ) ≤ x } = P { X − n p n p ( 1 − p ) ≤ x } = Φ ( x )
P\{\frac{X-E(X)}{\sqrt{D(X)}}\leq x\} = P\{\frac{X-np}{\sqrt{np(1-p)}}\leq x\} = \Phi(x)
P { D ( X ) X − E ( X ) ≤ x } = P { n p ( 1 − p ) X − n p ≤ x } = Φ ( x )
数理统计 请着重理清总体和样本的关系以及它们之间的计算,对于对于正态分布从期望和方差入手,牢记期望和方差的运算性质
A = ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) E ( A ) = n − 1 D ( A ) = 2 ( n − 1 )
A = \frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)\quad E(A)=n-1\quad D(A) = 2(n-1)
A = σ 2 ( n − 1 ) S 2 ∼ χ 2 ( n − 1 ) E ( A ) = n − 1 D ( A ) = 2 ( n − 1 )
卡方分布为标准正态分布的平方和分布,期望为自由度 n,方差为自由度的两倍 2n(所谓自由度就是参与卡方分布的标准正态分布的个数) t 分布为一个标准正态分布除以一个卡方分布,t 分布的自由度为其分布位置卡方分布的自由度 n F 分布为两个卡方分布除以自身自由度之商 卡方分布
χ ( n ) / n χ ( m ) / m ∼ F ( n , m )
\frac{\chi(n)/n}{\chi(m)/m} \sim F(n,m)
χ ( m ) / m χ ( n ) / n ∼ F ( n , m )
参数估计和假设检验 参数估计和无偏估计量 二阶原点矩估计,令
E ( X 2 ) = ∫ − ∞ + ∞ x 2 f ( x ) d x = A 2 = 1 n ∑ i = 1 n X i 2
E(X^2) = \int_{-\infty}^{+\infty}x^2f(x)dx = A_2 = \frac{1}{n}\sum_{i=1}^nX_i^2
E ( X 2 ) = ∫ − ∞ + ∞ x 2 f ( x ) d x = A 2 = n 1 i = 1 ∑ n X i 2
结合无偏估计量考察最大似然估计量,即求出最大似然估计后,再根据E(最大似然估计量)是否等于未知量本身,判断最大似然估计量是否无偏
这里通过期望将二者连续起来,好像就是在最大似然估计后用了一次矩估计进行判断?
t 检验 懂不了一点