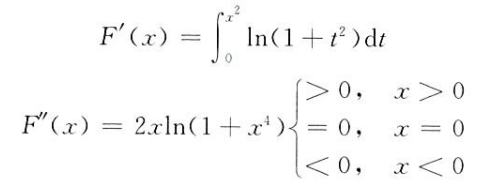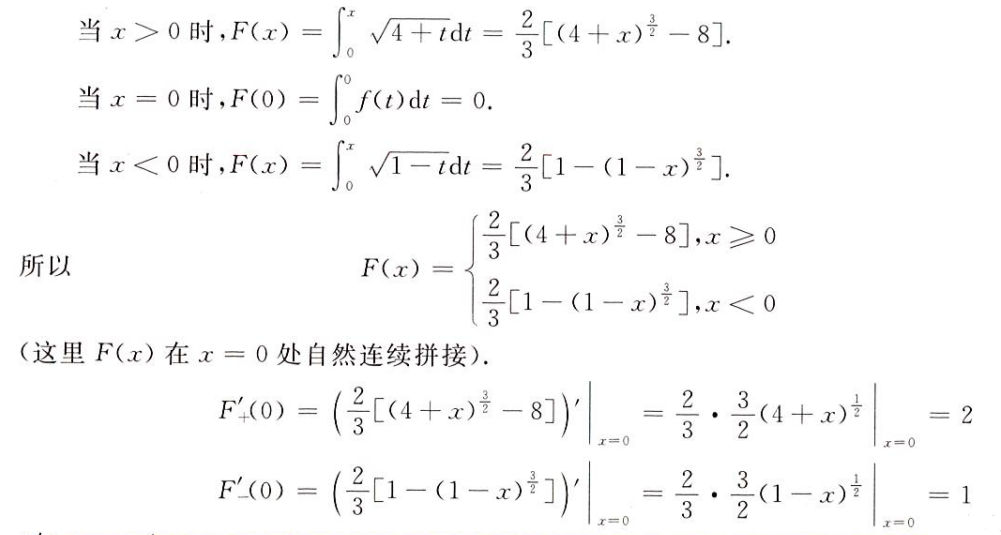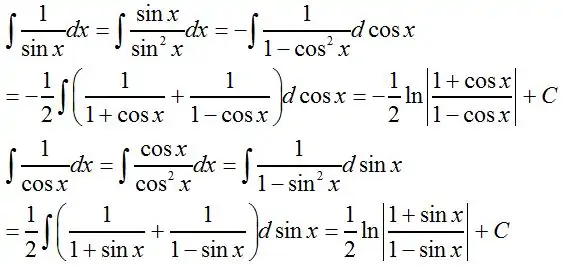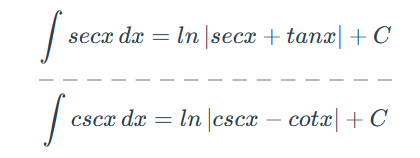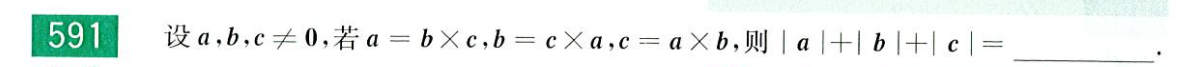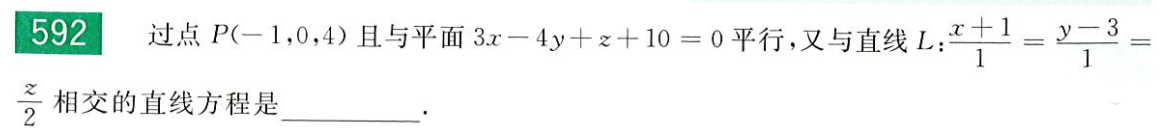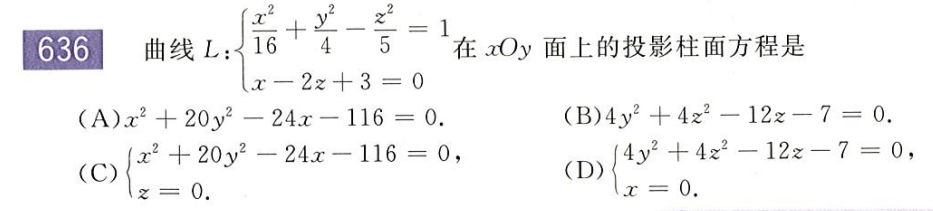一些遗漏的习题:T48、54、60~64、65、67~71
极限求解 数列、函数极限求解 就是一些常规方法:指、对、洛、等价(泰勒展开)
但要注意化简问题,如对于带根号的分式求极限,首先一定要考虑分子/分母有理化
对于数列,有时还有数学归纳法和放缩法的运用
泰勒展开求极限 泰勒展开的本质:通过 +/- 项使多项式逼近原函数
泰勒展开举例:就是对部分项展开,化简多项式,然后正常求极限
1、栗子一,对于下列极限
lim x → + ∞ ( 1 + 1 x ) x 2 e x = lim x → + ∞ e x 2 l n ( 1 + 1 x ) e x = lim x → + ∞ e x 2 l n ( 1 + 1 x ) − x
\lim_{x\rightarrow+\infty}\frac{(1+\frac{1}{x})^{x^2}}{e^x} =
\lim_{x\rightarrow+\infty}\frac{e^{x^2ln(1+\frac{1}{x})}}{e^x} =
\lim_{x\rightarrow+\infty}e^{x^2ln(1+\frac{1}{x})-x}
x → + ∞ lim e x ( 1 + x 1 ) x 2 = x → + ∞ lim e x e x 2 l n ( 1 + x 1 ) = x → + ∞ lim e x 2 l n ( 1 + x 1 ) − x x 2 l n ( 1 + 1 x )
x^2ln(1+\frac{1}{x})
x 2 l n ( 1 + x 1 ) lim x → 0 l n ( 1 + x ) = x − x 2 2 ! + . . .
\lim_{x\rightarrow0}ln(1+x) = x-\frac{x^2}{2!}+...
x → 0 lim l n ( 1 + x ) = x − 2 ! x 2 + ... lim x → 0 l n ( 1 + 1 x ) = 1 x − 1 2 x 2 + o ( x − 2 )
\lim_{x\rightarrow0}ln(1+\frac{1}{x}) = \frac{1}{x}-\frac{1}{2x^2}+o(x^{-2})
x → 0 lim l n ( 1 + x 1 ) = x 1 − 2 x 2 1 + o ( x − 2 ) x 2 l n ( 1 + 1 x ) − x = x − 1 2 − x = − 1 2
x^2ln(1+\frac{1}{x}) - x = x - \frac{1}{2} - x = -\frac{1}{2}
x 2 l n ( 1 + x 1 ) − x = x − 2 1 − x = − 2 1 e − 1 2
e^{-\frac{1}{2}}
e − 2 1 lim x → 0 a x 2 + b x + 1 − e x 2 − 2 x x 2 = 2
\lim_{x\rightarrow0}\frac{ax^2+bx+1-e^{x^2-2x}}{x^2} = 2
x → 0 lim x 2 a x 2 + b x + 1 − e x 2 − 2 x = 2 e x 2 − 2 x ⇒ 1 + ( x 2 − 2 x ) + ( x 2 − 2 x ) 2 2 + o ( x 2 )
e^{x^2-2x} \Rightarrow 1+(x^2-2x)+\frac{(x^2-2x)^2}{2}+o(x^2)
e x 2 − 2 x ⇒ 1 + ( x 2 − 2 x ) + 2 ( x 2 − 2 x ) 2 + o ( x 2 ) e x 2 − 2 x = 1 + 3 x 2 − 2 x + o ( x 2 )
e^{x^2-2x}= 1+3x^2-2x+o(x^2)
e x 2 − 2 x = 1 + 3 x 2 − 2 x + o ( x 2 ) lim x → 0 ( a − 3 ) x 2 + ( b + 2 ) x x 2 = 2
\lim_{x\rightarrow0}\frac{(a-3)x^2+(b+2)x}{x^2} = 2
x → 0 lim x 2 ( a − 3 ) x 2 + ( b + 2 ) x = 2 a-3 = 2, b = -2(x 前的系数一定要为 0,否则极限将为无穷)
连续、可导和可积 可导条件 T153
可导的两要素:连续(极限)、左右导数(连续不一定可导,可导一定连续)
连续不一定可导:连续指函数值连续,可导指函数导数连续(左右导数相等)
f(x) 连续,一定有 |f(x)| 连续,反之不成立
f ( x ) 连续 ⇒ ∣ f ( x ) ∣ 连续
f(x) 连续\Rightarrow |f(x)|连续
f ( x ) 连续 ⇒ ∣ f ( x ) ∣ 连续 f ( x ) 可导 ⇒ f ( x 2 ) 可导
f(x) 可导\Rightarrow f(x^2)可导
f ( x ) 可导 ⇒ f ( x 2 ) 可导
可积条件 T176、177、179、180、181
可积的三要素:连续、有界、间断点(可积不一定连续,连续一定可积)
可积的条件
充分但不必要:连续 充要:函数在范围内有界且在范围内间断点有限 如对于无界函数
f ( x ) = { t a n x , x ∈ ( − π 2 , π 2 ) 0 , x = ± π 2
f(x) =
\begin{cases}
tanx, x\in(-\frac{\pi}{2},\frac{\pi}{2})\\
0,\,x=\pm\frac{\pi}{2}
\end{cases}
f ( x ) = { t an x , x ∈ ( − 2 π , 2 π ) 0 , x = ± 2 π
如对于不连续函数
f ( x ) = s g n x = { 1 , x > 0 0 , x = 0 − 1 , x < 0
f(x) = sgn\,x =
\begin{cases}
1,\,x>0\\
0,\,x=0\\
-1,\,x<0
\end{cases}
f ( x ) = s g n x = ⎩ ⎨ ⎧ 1 , x > 0 0 , x = 0 − 1 , x < 0
还有,不可积的函数线性加上可积函数的复合函数,一定不可积,基于上述性质很容易理解
积分求导 一元积分导数 一元积分求导
∫ 0 x 2 f ( 2 u − 1 ) d u
\int_0^{x^2}f(2u-1)du
∫ 0 x 2 f ( 2 u − 1 ) d u 1 2 ∫ 0 x 2 f ( 2 u − 1 ) d ( 2 u − 1 ) = 1 2 ∫ − 1 2 x 2 − 1 f ( t ) d t
\frac{1}{2}\int_0^{x^2}f(2u-1)d(2u-1) = \frac{1}{2}\int_{-1}^{2x^2-1}f(t)dt
2 1 ∫ 0 x 2 f ( 2 u − 1 ) d ( 2 u − 1 ) = 2 1 ∫ − 1 2 x 2 − 1 f ( t ) d t [ 1 2 ∫ − 1 2 x 2 − 1 f ( t ) d t ] ’ = 1 2 f ( 2 x 2 − 1 ) 4 x
[\,\frac{1}{2}\int_{-1}^{2x^2-1}f(t)dt\,]’ = \frac{1}{2}f(2x^2-1)4x
[ 2 1 ∫ − 1 2 x 2 − 1 f ( t ) d t ] ’ = 2 1 f ( 2 x 2 − 1 ) 4 x
二元积分偏导 积分偏导
g ( x y ) = ∫ 1 x y f ( t ) d t
g(xy) = \int_1^{xy}f(t)dt
g ( x y ) = ∫ 1 x y f ( t ) d t ∂ f ∂ x = f ( x y ) y
\frac{∂f}{∂x} = f(xy)\,y
∂ x ∂ f = f ( x y ) y
连续积分求导 T193
对于二重积分
∫ 0 x ( ∫ 0 u 2 l n ( 1 + t 2 ) d t ) d u
\int_0^x(\int_0^{u^2}ln(1+t^2)dt)du
∫ 0 x ( ∫ 0 u 2 l n ( 1 + t 2 ) d t ) d u
导函数和原函数的联系 定理一:导函数 f(x) 若在 (a, b) 内连续,则原函数 F(x) 一定在 (a, b) 内可导且导数等于 f(x)
这里有点怪,既然已经知道了导函数,为什么还要说原函数有可能不可导呢?主要是由于区间限制,如
f ( x ) = { 4 + x x > 0 0 x = 0 1 − x x < 0
f(x) = \begin{cases}
\sqrt{4+x}&x>0\\
0&x=0\\
\sqrt{1-x}&x<0
\end{cases}
f ( x ) = ⎩ ⎨ ⎧ 4 + x 0 1 − x x > 0 x = 0 x < 0 通过分段的方式令其强行导函数值存在
故实际上 F(x) 在 x = 0 处左右导数并不相等,故该点不可导,只是对他的导函数 f(x) 进行了手动的分段处理,强行使 x = 0 处函数值相等
或者根据定理一也可以做出判断
这里 f(x) 在 x<0 和 x>0 的区间内均连续,所以在各自区间内一定有 F'(x) = f(x),于是
F(x) 有右导数
F + ′ ( 0 ) = f + ( 0 ) = lim x → 0 + f ( x ) = 4 + 0 + = 2
F'_+(0) = f_+(0) = \lim_{x\rightarrow0^+}f(x) = \sqrt{4+0^+}=2
F + ′ ( 0 ) = f + ( 0 ) = x → 0 + lim f ( x ) = 4 + 0 + = 2 F − ′ ( 0 ) = f − ( 0 ) = lim x → 0 − f ( x ) = 1 − 0 − = 1
F'_-(0) = f_-(0) = \lim_{x\rightarrow0^-}f(x) = \sqrt{1-0^-}=1
F − ′ ( 0 ) = f − ( 0 ) = x → 0 − lim f ( x ) = 1 − 0 − = 1
极值点和拐点的判定 极值点和拐点的判定从来不是等于 0,而是导函数正负号的突变,如在间断点 x0 左边导函数 f(x) 小于零,右边 f(x) 大于零,那么 x0 就是一个 F(x) 的极小值点(而这个点根本就没有定义)
从表面来看,拐点的判定有以下特征
从原函数来看,其凹凸性发生突变 从一阶导函数来看,原函数的拐点为一阶导的一个极值点 从二阶导函数来看,在拐点左右其正负值发生突变(根本原因) 一定要抓住:正负值突变是取极值或拐点的本质原因,而间断点和极值点/拐点并没有必然联系,导函数为 0 和极值点/拐点也没有必然联系
不定积分和定积分 积分大小判定和中值定理 T184、185
考虑被积函数的大小,结合中值定理
( b − a ) f ( ξ ) = ∫ a b f ( x ) d x ξ ∈ ( a , b )
(b-a)f(\xi) = \int_a^bf(x)dx\quad \xi\in(a,b)
( b − a ) f ( ξ ) = ∫ a b f ( x ) d x ξ ∈ ( a , b ) f ( x ) = s i n x x x ∈ ( 0 , π 2 )
f(x) = \frac{sinx}{x}\quad x\in(0,\frac{\pi}{2})
f ( x ) = x s in x x ∈ ( 0 , 2 π ) f ′ ( x ) = x c o s x − s i n x x 2 < 0
f'(x) = \frac{xcosx-sinx}{x^2} < 0
f ′ ( x ) = x 2 x cos x − s in x < 0 f m i n ( x ) = f ( π 2 ) = 2 π
f_{min}(x) = f(\frac{\pi}{2}) = \frac{2}{\pi}
f min ( x ) = f ( 2 π ) = π 2 ∫ 0 π 2 f ( x ) d x ≥ ( π 2 − 0 ) f m i n = 1
\int_0^{\frac{\pi}{2}}f(x)dx \geq (\frac{\pi}{2}-0)f_{min} = 1
∫ 0 2 π f ( x ) d x ≥ ( 2 π − 0 ) f min = 1 f ( x ) = x s i n x > s i n x x
f(x) = \frac{x}{sinx} > \frac{sinx}{x}
f ( x ) = s in x x > x s in x ∫ 0 π 2 x s i n x d x > ∫ 0 π 2 s i n x x ≥ 1
\int_0^{\frac{\pi}{2}}\frac{x}{sinx}dx > \int_0^{\frac{\pi}{2}}\frac{sinx}{x} \geq 1
∫ 0 2 π s in x x d x > ∫ 0 2 π x s in x ≥ 1
反常积分的收敛判断 定积分要求
而反常积分即为破坏上述任意一个条件的定积分,分为
无穷限积分 瑕积分:被积函数在某点无界,该点称为瑕点,如 lnx 在 x=0 处 就是积分,然后判断瑕点是否积分值是否存在(不存在即为趋于无穷),或判断无穷限时,函数值是否存在
三角积分 sinx 分之一的积分,通过手动对补一个 sinx,分母通过 1 化为 cosx,分子放在微分符号后面,积为 cosx,然后对这个 cosx 进行拆分,并进行对数积分,得到结果
cosx 是对 sinx 对数积分,分子为 +,分母为 - sinx 是对 cosx 对数积分,分子为 -,分母为 + 别忘了系数 1/2
等价于
根号下三角函数处理,通过倍角公式消去 1 以及用平方抵消根号
1 − c o s x = 1 − ( 1 − 2 s i n 2 x 2 ) = 2 s i n x 2
\sqrt{1-cosx} = \sqrt{1-(1-2sin^2\frac{x}{2})} = \sqrt2sin\frac{x}{2}
1 − cos x = 1 − ( 1 − 2 s i n 2 2 x ) = 2 s in 2 x
举个栗子
常见积分技巧 e 的 y 次方的积分次序交换 对于二重积分
∫ 0 1 d x ∫ x 1 e y 2 d y
\int_0^1dx\int_x^1e^{y^2}dy
∫ 0 1 d x ∫ x 1 e y 2 d y ∫ 0 1 d y ∫ 0 y e y 2 d x
\int_0^1dy\int_0^ye^{y^2}dx
∫ 0 1 d y ∫ 0 y e y 2 d x
巧用分部积分 对一个二重积分使用分部积分
微积分物理应用 参数方程旋转体 旋转体体积求解,其实和普通方程一样,普通方程公式为
π ∫ a b y 2 d x
\pi\int_a^b y^2dx
π ∫ a b y 2 d x
化为参数方程即为
π ∫ t 1 t 2 y 2 ( t ) d x ( t )
\pi\int_{t_1}^{t_2}y^2(t)\,dx(t)
π ∫ t 1 t 2 y 2 ( t ) d x ( t )
旋转体面积求解,首先要明确弧长公式
s = ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t
s = \int\sqrt{x'(t)^2+y'(t)^2}dt
s = ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t 2 π ∫ ∣ y ( t ) ∣ x ′ ( t ) 2 + y ′ ( t ) 2 d t
2\pi\int|y(t)|\sqrt{x'(t)^2+y'(t)^2}dt
2 π ∫ ∣ y ( t ) ∣ x ′ ( t ) 2 + y ′ ( t ) 2 d t
梯度和方向导数 对于一个多元函数,其梯度为各偏导组成的一维向量,如
f ( x , y ) = x 2 + 2 x + y 2 + y + 1
f(x,y) = x^2+2x+y^2+y+1
f ( x , y ) = x 2 + 2 x + y 2 + y + 1 ∂ f ∂ x = 2 x + 2 ∂ f ∂ y = 2 y + 1
\frac{∂f}{∂x} = 2x+2\quad \frac{∂f}{∂y} = 2y+1
∂ x ∂ f = 2 x + 2 ∂ y ∂ f = 2 y + 1 g r a d ( f ) = [ 2 x + 2 , 2 y + 1 ]
grad(f) = [2x+2,\,2y+1]
g r a d ( f ) = [ 2 x + 2 , 2 y + 1 ] g r a d ( f ) ∣ ( 1 , 1 ) = [ 4 , 3 ]
grad(f)_{|(1,1)} = [4, 3]
g r a d ( f ) ∣ ( 1 , 1 ) = [ 4 , 3 ] l = [ 1 , 7 ]
l = [1,7]
l = [ 1 , 7 ] g r a d ( f ) ⋅ l T = 2 x + 2 + 14 y + 7 = 2 x + 14 y + 9
grad(f) \cdot l^T = 2x+2+14y+7 = 2x+14y+9
g r a d ( f ) ⋅ l T = 2 x + 2 + 14 y + 7 = 2 x + 14 y + 9
质心 在二维坐标系下,一个图形的质心的横坐标为
x ‾ = ∫ x ( t ) x ′ ( t ) 2 + y ′ ( t ) 2 d t ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t
\overline{x} = \frac{\int x(t)\sqrt{x'(t)^2+y'(t)^2}dt}{\int\sqrt{x'(t)^2+y'(t)^2}dt}
x = ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t ∫ x ( t ) x ′ ( t ) 2 + y ′ ( t ) 2 d t y ‾ = ∫ y ( t ) x ′ ( t ) 2 + y ′ ( t ) 2 d t ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t
\overline{y} = \frac{\int y(t)\sqrt{x'(t)^2+y'(t)^2}dt}{\int\sqrt{x'(t)^2+y'(t)^2}dt}
y = ∫ x ′ ( t ) 2 + y ′ ( t ) 2 d t ∫ y ( t ) x ′ ( t ) 2 + y ′ ( t ) 2 d t
空间解析几何 内积和叉积 当两向量垂直(其夹角为 90°),二者的叉积的模长等于两向量模长之积
∣ c ∣ = ∣ a ∣ ∣ b ∣ s i n < a , b >
|c| = |a|\,|b|\,sin<a,b>
∣ c ∣ = ∣ a ∣ ∣ b ∣ s in < a , b >
举个栗子
此时已知 a、b、c 两两垂直,且
∣ a ∣ = ∣ b ∣ ∣ c ∣ ∣ c ∣ = ∣ a ∣ ∣ b ∣ ⟶ ∣ a ∣ = ∣ a ∣ ∣ b ∣ 2 ⇒ ∣ b ∣ = 1
|a| = |b|\,|c|\quad |c|=|a|\,|b|\longrightarrow |a|=|a|\,|b|^2 \Rightarrow |b| = 1
∣ a ∣ = ∣ b ∣ ∣ c ∣ ∣ c ∣ = ∣ a ∣ ∣ b ∣ ⟶ ∣ a ∣ = ∣ a ∣ ∣ b ∣ 2 ⇒ ∣ b ∣ = 1 |a|+|b|+|c| = 1+1+1 = 3
用内积可以求两直线夹角
a b = ∣ a ∣ ∣ b ∣ c o s < a , b >
ab=|a|\,|b|\,cos<a,b>
ab = ∣ a ∣ ∣ b ∣ cos < a , b >
求解投影 对于平面来说,其法向量就是各未知数前系数所组成的向量,如
a x − b y + c z + d = 0 ⇒ n → = ( a , − b , c )
ax-by+cz+d = 0\Rightarrow \mathop{n}^{\rightarrow}=(a,-b,c)
a x − b y + cz + d = 0 ⇒ n → = ( a , − b , c ) { 2 y + 3 z − 5 = 0 x − 2 y − z + 7 = 0 ⇒ s → = ∣ i j k 0 2 3 1 − 2 − 1 ∣ = ( 4 , 3 , − 1 )
\begin{cases}
2y+3z-5=0\\
x-2y-z+7=0
\end{cases}
\Rightarrow
\mathop{s}^{\rightarrow}=
\left | \begin{matrix}
i&j&k\\
0&2&3\\
1&-2&-1
\end{matrix} \right |
= (4,3,-1)
{ 2 y + 3 z − 5 = 0 x − 2 y − z + 7 = 0 ⇒ s → = i 0 1 j 2 − 2 k 3 − 1 = ( 4 , 3 , − 1 ) L : x + 1 1 = y − 3 1 = z 2 ⇒ s → = ( 1 , 1 , 2 )
L:\frac{x+1}{1}=\frac{y-3}{1}=\frac{z}{2}\Rightarrow\mathop{s}^{\rightarrow}=(1,1,2)
L : 1 x + 1 = 1 y − 3 = 2 z ⇒ s → = ( 1 , 1 , 2 )
通过直线的方向向量和平面的法向量,可以做出一个垂直于平面的新平面
通过方向向量和原平面法向量叉积求出新平面的法向量 再通过直线上一点列出平面方程 这里新平面和原平面的交线,也就是直线在原平面上的一个投影,当然可以用新旧两平面交线形式表达出来
通过 L 方程可求其方向向量
s → = ∣ i j k 0 2 3 1 − 2 − 1 ∣ = ( 4 , 3 , − 1 )
\mathop{s}^{\rightarrow}=
\left | \begin{matrix}
i&j&k\\
0&2&3\\
1&-2&-1
\end{matrix} \right |
= (4,3,-1)
s → = i 0 1 j 2 − 2 k 3 − 1 = ( 4 , 3 , − 1 ) s → = ∣ i j k 4 3 − 1 1 − 1 3 ∣ = ( 1 , − 2 , − 1 )
\mathop{s}^{\rightarrow}=
\left | \begin{matrix}
i&j&k\\
4&3&-1\\
1&-1&3
\end{matrix} \right |
= (1,-2,-1)
s → = i 4 1 j 3 − 1 k − 1 3 = ( 1 , − 2 , − 1 ) x − 2 ( y − 4 ) − ( z + 1 ) = 0 ⟹ x − 2 y − z + 7 = 0
x-2(y-4)-(z+1)=0\Longrightarrow x-2y-z+7=0
x − 2 ( y − 4 ) − ( z + 1 ) = 0 ⟹ x − 2 y − z + 7 = 0 L ′ = { x − 2 y − z + 7 = 0 x − y + 3 z + 8 = 0
L'=\begin{cases}
x-2y-z+7=0\\
x-y+3z+8=0
\end{cases}
L ′ = { x − 2 y − z + 7 = 0 x − y + 3 z + 8 = 0
法向量、方向向量和平行平面 求解与某平面平行且与某直线相交且过某点的直线方程
求解步骤如下
过点 P 做平面 Ⅰ 的平行平面 Ⅱ,易知 Ⅱ 上任何直线均平行于 Ⅰ 只要在 Ⅱ 上找到一条过 P 和 L 的直线,即为题目所求
先要找到直线 L 和平面 Ⅱ 的交点 Q 通过直线上两点,即 P 和 Q,写出直线方程 Ⅱ 方程可以直接写出
3 ( x + 1 ) − 4 y + ( z − 4 ) = 0 ⟹ 3 x − 4 y + z + 1 = 0
3(x+1)-4y+(z-4) = 0\Longrightarrow 3x-4y+z+1=0
3 ( x + 1 ) − 4 y + ( z − 4 ) = 0 ⟹ 3 x − 4 y + z + 1 = 0 k = ( 15 + 1 , 19 − 0 , 32 − 4 ) = ( 16 , 19 , 28 )
k=(15+1,19-0,32-4)=(16,19,28)
k = ( 15 + 1 , 19 − 0 , 32 − 4 ) = ( 16 , 19 , 28 ) L ′ : x + 1 16 = y 19 = z − 4 28
L':\frac{x+1}{16}=\frac{y}{19}=\frac{z-4}{28}
L ′ : 16 x + 1 = 19 y = 28 z − 4
空间中两点直线方程 已知 P Q 两点为
P ( a 1 , b 1 , c 1 ) Q ( a 2 , b 2 , c 2 )
P(a_1,b_1,c_1)\quad Q(a_2,b_2,c_2)
P ( a 1 , b 1 , c 1 ) Q ( a 2 , b 2 , c 2 ) x − a 1 a 2 − a 1 = y − b 1 b 2 − b 1 = z − c 1 c 2 − c 1
\frac{x-a_1}{a_2-a_1}=\frac{y-b_1}{b_2-b_1}=\frac{z-c_1}{c_2-c_1}
a 2 − a 1 x − a 1 = b 2 − b 1 y − b 1 = c 2 − c 1 z − c 1
求解旋转体方程 总体来说,是一个设原点,根据旋转特性列方程,消除原点未知数的过程
设 L 上任意一点P(x0,y0,z0),经旋转后到达点Q(x,y,z),二者坐标一定满足
{ z 0 = z ( x 0 − 2 ) 2 + ( y 0 − 3 ) 2 = ( x − 2 ) 2 + ( y − 3 ) 2
\begin{cases}
z_0=z\\
(x_0-2)^2+(y_0-3)^2=(x-2)^2+(y-3)^2
\end{cases}
{ z 0 = z ( x 0 − 2 ) 2 + ( y 0 − 3 ) 2 = ( x − 2 ) 2 + ( y − 3 ) 2 x 3 − 3 2 = y 0 − 1 3 = z 0 + 1
\frac{x_3-3}{2}=\frac{y_0-1}{3}=z_0+1
2 x 3 − 3 = 3 y 0 − 1 = z 0 + 1 (x0,y0,z0)即得关于(x,y,z)坐标满足的方程,即为所求曲面方程
x 2 + y 2 − 13 z 2 − 4 x − 6 y − 18 z + 3 = 0
x^2+y^2-13z^2-4x-6y-18z+3=0
x 2 + y 2 − 13 z 2 − 4 x − 6 y − 18 z + 3 = 0
点到平面距离 对于平面ax + by + cz + d = 0和点(x,y,z),其距离为
d = ∣ a x + b y + c z + d ∣ ∣ n ∣ ∣ n ∣ = a 2 + b 2 + c 2
d=\frac{|ax+by+cz+d|}{|n|}\quad |n|=\sqrt{a^2+b^2+c^2}
d = ∣ n ∣ ∣ a x + b y + cz + d ∣ ∣ n ∣ = a 2 + b 2 + c 2 (a,b,c),半径为r ( x − a ) 2 + ( y − b ) 2 + ( z − c ) 2 = r 2
(x-a)^2+(y-b)^2+(z-c)^2=r^2
( x − a ) 2 + ( y − b ) 2 + ( z − c ) 2 = r 2
求解标准平面上的柱面 就是把曲线的某一个自变量消掉,如把 z 消掉,即为在 xOy 平面上的柱面方程
直接通过第二个平面方程
z = x + 3 2
z = \frac{x+3}{2}
z = 2 x + 3 x 2 16 + y 2 4 − ( x + 3 ) 2 2 2 × 5 = 1
\frac{x^2}{16}+\frac{y^2}{4}-\frac{(x+3)^2}{2^2\times5}=1
16 x 2 + 4 y 2 − 2 2 × 5 ( x + 3 ) 2 = 1 x 2 + 20 y 2 − 24 x = 116
x^2+20y^2-24x=116
x 2 + 20 y 2 − 24 x = 116
共面、平行和重合