离散型随机变量及其分布

随机事件和概率

随机事件、事件间的关系与运算

一些名词解释

• 随机试验（试验）：可重复性
• 样本点和样本空间：试验结果
• 随机事件（事件）：样本空间子集

随机事件的关系
包含	⊂ 箭头指向谁，谓语是谁，如 A ⊂ B 则 B 包含 A
相等	互相包含
互斥	不相容，不同时发生
对立	A 不发生 B 必发生
独立	P(AB) = P(A)P(B)

随机事件的运算
交（积）	都发生，A ∩ B，AB
并（和）	至少一个发生，A∪B，或 A+B
差	A - B，A 发生 B 不发生

独立的性质：若事件 A B 独立，则

$$P(AB) = P(A)P(B)$$

并的拆分

$$P(A+B) = P(A)+P(B)-P(AB)\\ ----------------\\ P(A+B+C) = P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)$$

并运算的分配律

$$P[(A+B)(A+B)] = P(A)+2P(AB)+P(B)$$

其中

$$P(AA) = P(A)\quad P(AB) = P(BA)$$

总的来说求随机事件概率

• 一是画图
• 二是运算

独立和不相容的区别

• 不相容：P(AB) = 0
• 独立：P(AB) = P(A)P(B)

概率及概率公式

和高中内容是否有些许重合

古典概型与伯努利概型

伯努利方程（一种一阶微分方程），将只相差 1 的两个 y 的幂用高次的微分代替，这样方程中将只含有一个关于 y 的幂，将这个 y 的幂设为新的未知函数 z，用公式法求解一阶线性微分方程得到 z，反代回去最终得到 y

离散随机变量概述

一维随机变量的分布、概率密度、数学期望以及方差

一维离散随机分布

形如这样的分布即为一维离散随机分布

X	0	1
P	0.5	0.5

很显然，这里的自变量只有 X 一个，即一个 X 对应一个概率，故为一维分布

二维离散随机分布

二位随机分布，其自变量为两个 X 和 Y，二者共同决定一个概率

其实就是这样一个二维表

X\Y	Y1	Y2	...	Yn	...
X1	P11	P12		P1n
X2	P21	P22		P2n
...
Xn	Pn1	Pn2		Pnn
...

性质如下

$$0 \leq P_{ij} \leq 1 \quad\quad \sum P_{ij} = 1$$

联合分布列和边际分布列

联合分布列，就是联合概率分布表

边际分布列，就是单个变量的概率分布表，塌陷二维分布中其中一个变量便可以得到另一变量的边际分布

X	x1	x2	...	xn	...
P	P1-	P2-		Pn-

Y	y1	y2	...	yn	...
P	P-1	P-2		P-n

离散随机变量的独立

事件独立：有事件a,b，若P(a,b) = P(a)P(b)，则事件a,b相互独立

二维离散随机变量的独立：对于二维随机变量的联合分布表，每个概率Pij都为两个变量相应的边际分布概率相乘

如 X/Y 有边际分布

X	0	1
P	0.4	0.6

Y	0	1
P	0.3	0.7

其联合分布为

X\Y	0	1
0	0.12	0.28
1	0.18	0.42

其中

$$P_{00} = P_{x=0}\,P_{y=0} = 0.4\times0.3 = 0.12\\ P_{01} = P_{x=0}\,P_{y=1} = 0.4\times0.7 = 0.28\\ P_{10} = P_{x=1}\,P_{y=0} = 0.6\times0.3 = 0.18\\ P_{11} = P_{x=1}\,P_{y=1} = 0.6\times0.7 = 0.42$$

此时我们说二维离散随机变量 X/Y 是独立的

离散型随机变量函数的分布

随机变量函数的定义

随机变量函数：一个二元函数，自变量、因变量均为随机变量，函数映射的是他们的值，而不是概率

• 概率由自变量传递给因变量
• 相同值的概率是可以合并的

对于下列一维离散随机变量

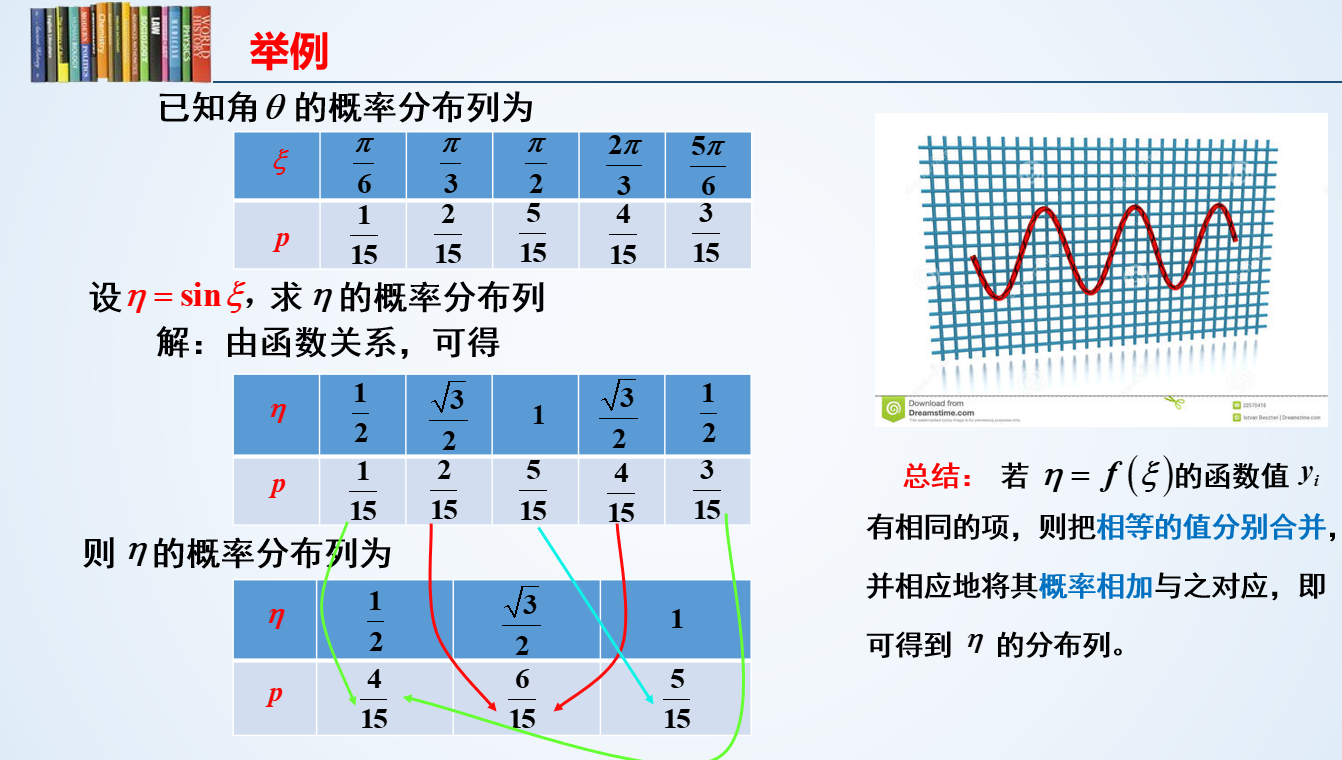
实际上就是一个正常的二元函数，只不过每个自变量取值将其原有附带的概率也传递给了因变量（随机变量函数）

离散随机变量函数

对于二维随机变量 X/Y 的分布表

X\Y	0	1
1	0.2	0.3
2	0.4	0.1

现在有这样一个函数：f = X+Y

那么这个函数f实际上塌陷为一个一维随机变量，其相对应的概率分布表（一维）为

f	1	2	3
P	0.2	0.7	0.1

当f = X + Y = 1 + 0 = 1时，概率为0.2

当f = X + Y = 2时，有两种可能，一为Y = 1, X = 1，二为Y = 0, X = 2，所以P(f=2)为二者概率相加，即0.3+0.4=0.7

当f = X+Y = 2+1 = 3时，概率为0.1

常见离散随机变量概率分布

二项分布

在n次独立重复的伯努利试验中，设每次试验中事件A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数，则X的可能取值为0，1，…，n，且对每一个k（0≤k≤n）,事件{X=k}即为n次试验中事件A恰好发生k次，随机变量X的离散概率分布即为二项分布（Binomial Distribution）

举个栗子：如抛硬币n次，花面次数X的概率分布（花面概率p始终为0.5）

用符号b表示二项分布：X ~ b(n,p)表示进行次数为n，抛硬币 m 次画面次数 H 的二项分布表示为H ~ (m,0.5)

数学期望：每次独立事件发生概率均为p的二项分布X，其数学期望为np

0-1分布

当二项分布X ~ b(n,p)中n=1时，即只进行一次实验，事件发生次数要么1次要么0次（如抛一次硬币），即为0-1分布，其数学期望为p(n=1)

其分布列为

X	1	0
P	0.5	0,5

泊松分布

泊松分布的概率函数，记为 P(λ)

$$P(x=k)=\frac{\lambda ^k}{k!}e^{-\lambda}$$

• λ为单位时间(或单位面积)内随机事件的平均发生次数，是泊松分布的唯一参数
• 泊松分布适合于描述单位时间内随机事件发生的次数

泊松分布的数学期望和方差均为λ

几何分布

几何分布（Geometric distribution）。一种定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。详细地说，是：前k-1次皆失败，第 k 次成功的概率

• 简单来说，就是抛硬币第i次首次抛到花面的概率分布

几何分布表示为：X ~ Ge(p)

• 其中p为每次独立实验事件发生的概率

其数学期望为E(X) = 1/p