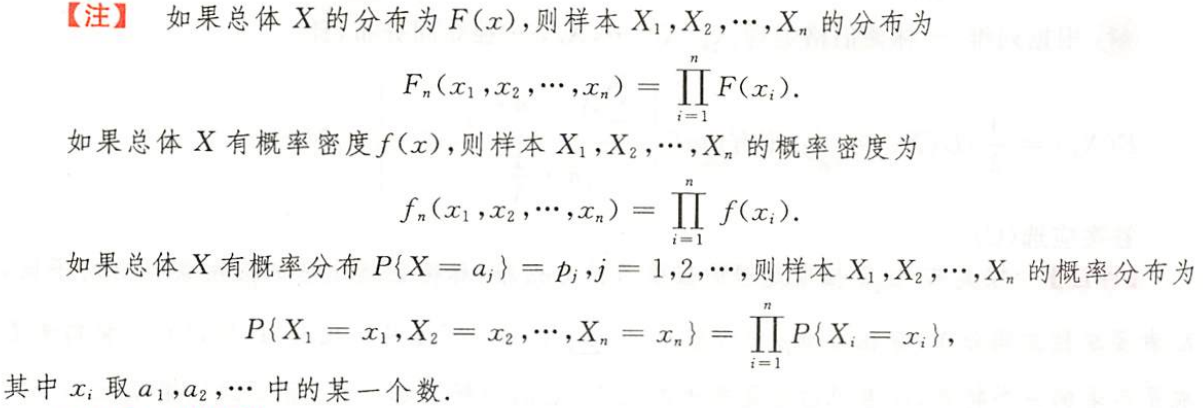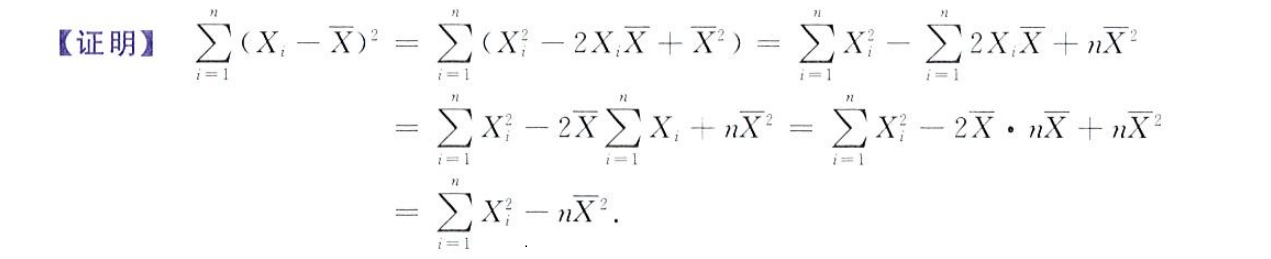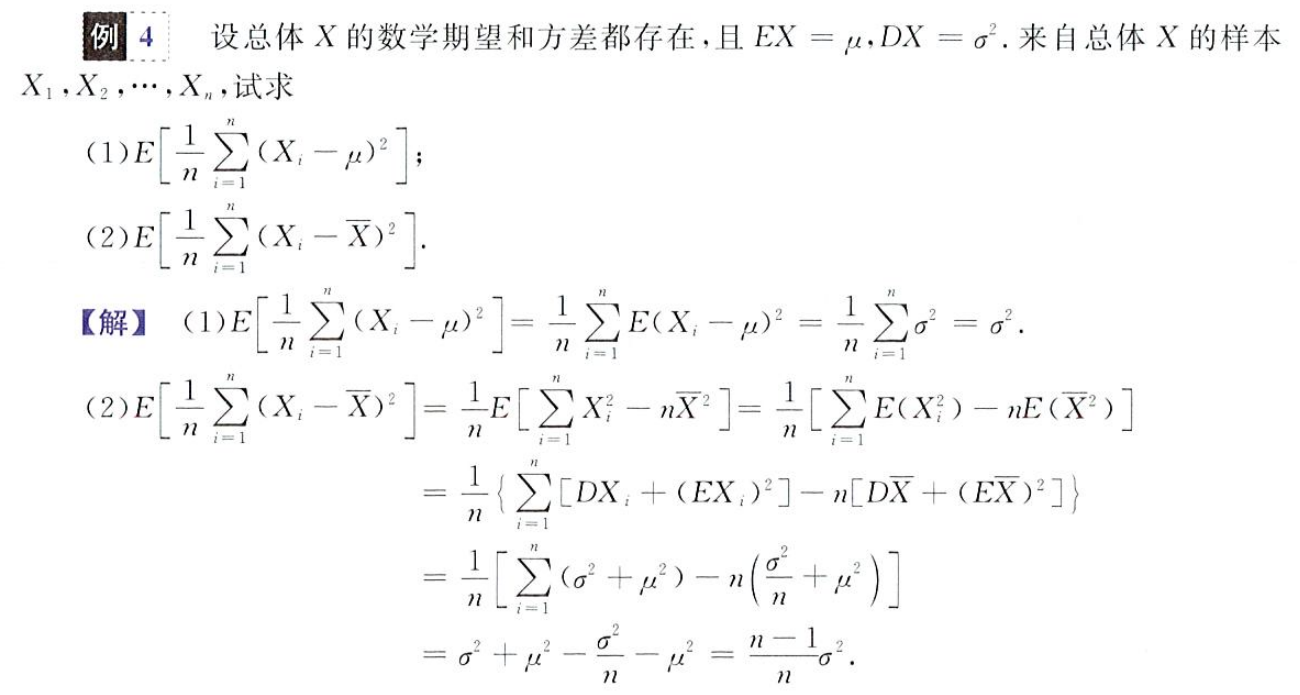在实际应用中,很多情况事先并不知道随机变量的分布函数是什么,有的时候即便知道服从什么样的分布类型,但是却不清楚具体的参数是什么,这就需要借助于统计的知识加以明确
统计学:以偏概全
总体、样本和统计量和样本数字特征
总体和样本的定义
基本概念
- 总体:研究对象的某项数量指标 X 的全体
- 个体:研究对象中某一个对象的指标叫做个体
- 样本:如果
(X1,X2,...,Xn)相互独立且与总体 X 同分布,则(X1,X2,...,Xn)为来自 X 的简单随机样本,简称样本,n为样本容量 - 样本观察值:简单随机样本
Xi具体取值的集合(x1,x2,...,xn)称作样本观察值
总体和样本的关系
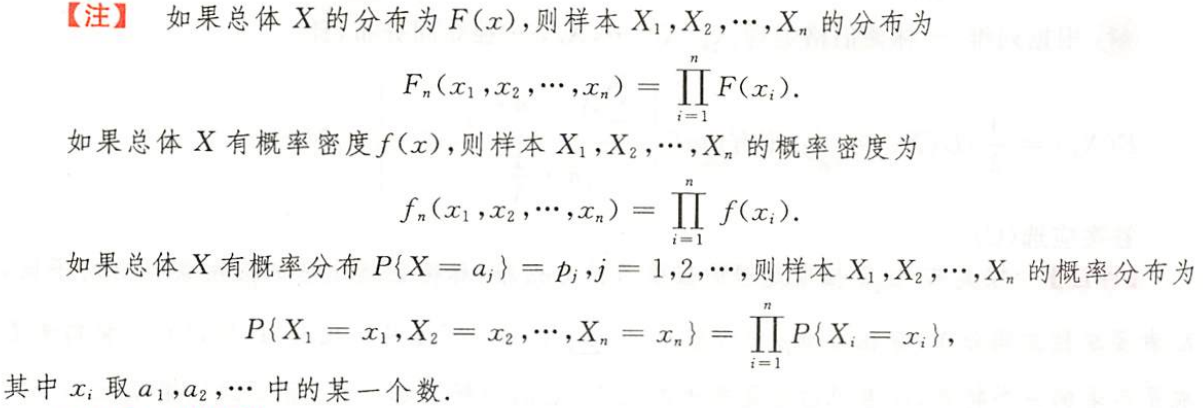
取样有点像一个独立重复实验?或者说其实就是,其概率和分布自然通过相乘来合并
举两个栗子


常见统计量
统计量:(X1,X2,...,Xn)为来自于总体 X 的样本,(X1,X2,...,Xn)的不含未知参数的表达式为 X 的统计量,如
3X1+X2+X3,X12+X22+X32,aX1+2X2−X3
其中第一、二是统计量,第三不是统计量。统计量是无穷无尽的,但有价值的统计量并不多:如特朗普和我,我没有统计价值,而特朗普有
样本均值(期望)
X=n1i=1∑nXi
样本方差和标准差
S2=n−11i=1∑n(Xi−X)S=n−11i=1∑n(Xi−X)
样本的 k 阶原点距
Ak=n1i=1∑nXik
样本的 k 阶中心距
Bk=n1i=1∑n(Xi−X)kB2=nn−1S2=S2
1 阶原点距即为样本均值,2 阶原点距为
A2=n1(x12+x22+...+xk2)
一个常用推论
i=1∑n(Xi−X)2=i=1∑nXi2−nX2 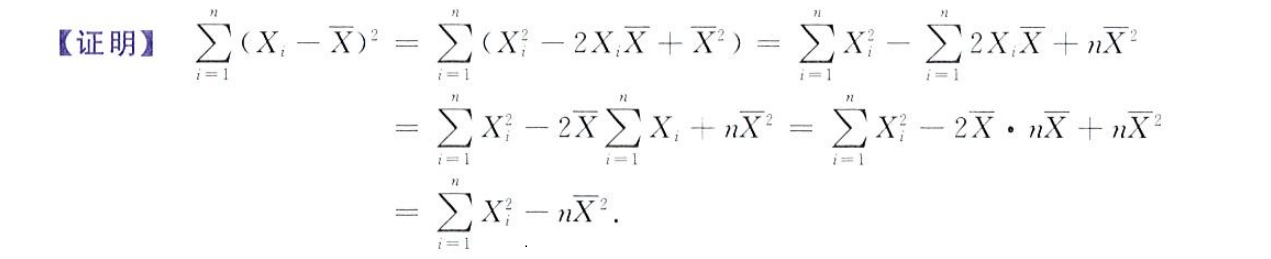
这里的求和可以在 i 前任意调换位置,就像幂级数的变换,将原式换算为已知值,如样本均值、方差,以此来推进运算
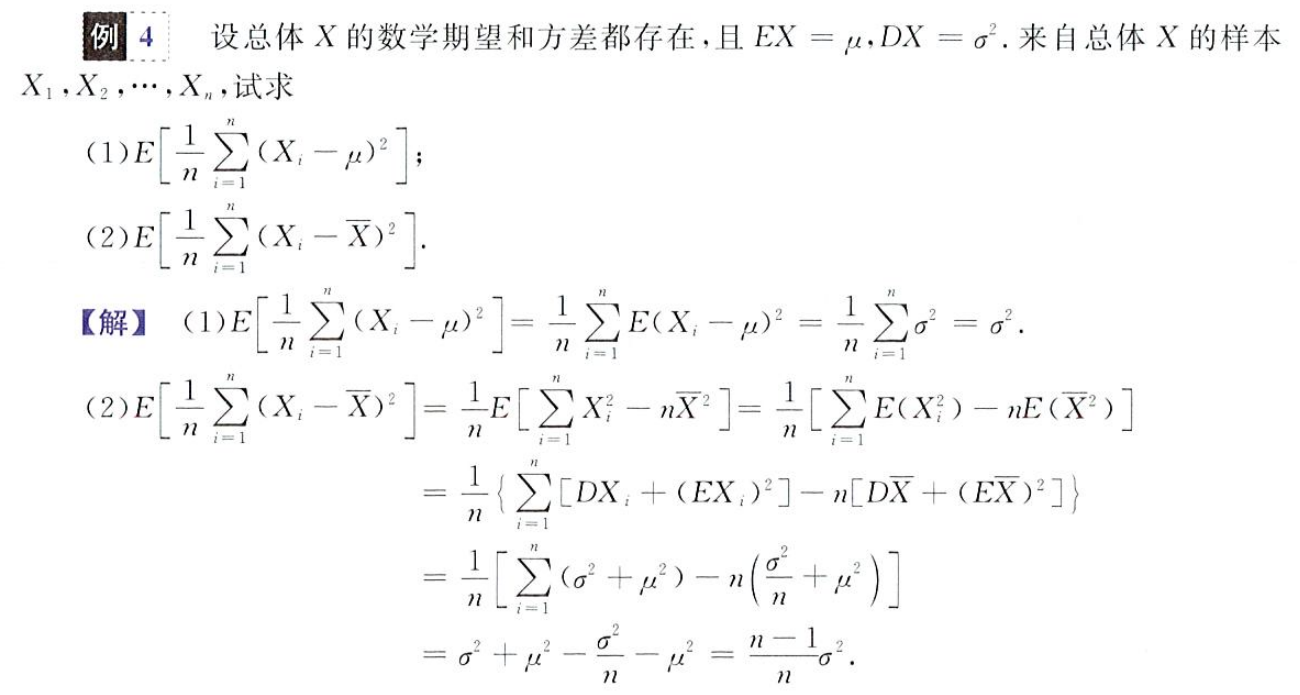
对于总体为 0/1 分布的 X,其样本独立重复实验,就相当于一个伯努利实验,其样本之和(概率直接相乘)满足二项分布

常见统计抽样分布
就是一些常见的样本统计量,针对为正态分布的总体
回顾一下正态分布(接下来介绍的三个抽样分布都基于服从标准正态分布的总体)
若总体X~N(0,1),即服从标准正态分布
则其样本(X1,X2,...,Xn)
对于总体X~N(2,8),现有样本X1,X2遵循总体分布,则
aX1+bX2∼N(2a+2b,8a2+8b2)→22a2+2b2(aX1+bX2)−(2a+2b)∼N(0,1)
卡方分布
卡方分布定义
标准正态分布的平方和
(X1,X2,...,Xn)均相互独立且服从标准正态分布,则
X12+X22+...+Xn2∼χ2
- 随机变量的平方仍为随机变量
- 随机变量的和仍为随机变量
定义若干标准正态分布的平方和构成的随机变量服从卡方分布
卡方分布的性质
维数为1的卡方分布就是标准正态分布的平方
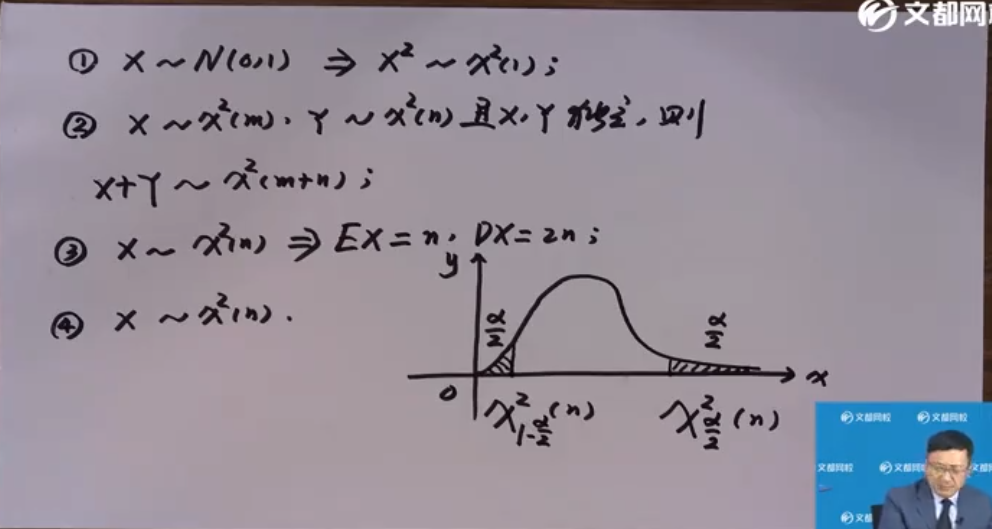
X∼N(0,1)→X2∼χ2(1)
两个独立的塌方分布相加,其结果的随机变量为他们维数之和的卡方分布
X∼X2(m),Y∼X2(n),X⊥Y→X+Y∼X2(m+n)
卡方分布的期望为其维数n,方差为维数的两倍,即2n X∼X2(n)→E(X)=n,D(X)=2n
右范围点和左范围点,对于卡方分布的密度函数,对于其面积为a/2的点,从右向左的横坐标记为右范围点,从左向右的横坐标记为左范围点
X1−2α2X2α2
对于非标准正态分布的总体X ~ N(u,a^2)
其样本(X1,X2,...,Xn)同样服从N(u,a^2)
根据标准化:
σXi−u∼N(0,1)
则
(σX1−u)2+(σX2−u)2+...+(σXn−u)2∼X2(n)
即
σ21i=1∑n(Xi−u)2∼X2(n)
t 分布
t 分布定义
t 分布是标准正态分布和卡方分布的商
前提条件
X∼N(0,1),Y∼X2(n),X⊥Y
将上述标准正态分布和卡方分布做如下除法得
nYX=τ∼t(n)
例题:设有总体X~N(0,4),现有样本X1,X2,X3,X4,问
A=X32+X42X1−X2∼?
上述随机变量A属于什么分布?
考虑分子
X1−X2∼N(0,8)→22X1−X2∼N(0,1)
考虑分母
X3∼N(0,4)→2X3∼N(0,1)→4X32+X42∼X2(2)
用一个正态分布除以卡方分布开根,得t分布
U=4X32+X42×2122X1−X2=X32+X42X1−X2∼X2(2)
完全符合,其中1/2就是那个常数1/n,X是一个标准正态分布,Y是一个n维的卡方分布
nYX=τ∼t(n)
t 分布的性质
对于一个 t 分布,有
t 分布的密度关于 y 轴对称,即为偶函数,和卡方分布一样有左右范围点,并且满足
t1−2αn=−t2αn
F 分布
F 分布定义
F 分布为两个卡方分布的商
前提条件
X∼X2(m),Y∼X2(n),X⊥Y
将两个卡方分布做如下除法得
Y/nX/m∼F(m,n)
其中m,n称为自由度
例题
U∼t(3)U2∼?
t分布是标准正态分布和卡方分布的商
U=Y/3XX∼N(0,1),Y∼X2(3)
则有
U2=Y/3X2/1
又因为
X2∼X2(1),Y∼X2(3)
所以
U2∼F(1,3)
F 分布的性质
F 分布的倒数同样为 F 分布,一二维度交换位置
X∼F(m,n)→X1∼F(n,m)
F分布的密度函数,分为左右范围点
F1−2α(m,n)F2α(m,n)
当0 < α < 1,对于两个F分布的范围点有如下关系
F1−α(m,n)=Fα(m,n)1
正态总体的抽样分布
好难,这个地方化来化去
设X~N(u,a^2),取出样本(X1,X2,...,Xn),各个体相互独立并且和总体分布相同
样本均值为
X=n1X1+n1X2+...+n1Xn
易知这个均值同样是一个正态分布
根距正态分布相加的规则
aX1+bX2∼N(au+bu,a2σ2+b2σ2)
可得
X∼N(u,nσ2)
则均值的期望和方差分别为:正态分布期望为u,方差为v^2 E(X)=uD(X)=nσ2
将均值标准化可得
nσX−u∼N(0,1)(1)
其中σ是总体的均方差(方差开根),将这个sigma换成样本的均方差S,可得
nSX−u∼t(n−1)(2)
之前已经推过,对于一个不标准的正态分布序列(X1,X2,...,Xn), Xi ~ N(u,a^2),有平方和服从卡方分布的特点
σ21i=1∑n(Xi−u)2=σ2(X1−u)2+...+σ2(Xn−u)2∼X2(n)(3)
上式中,u是总体期望(均值),将这个u换成样本均值,可得
σ21i=1∑n(Xi−X)2∼X2(n−1)
乘除变换得
σ2n−1n−11i=1∑n(Xi−X)2∼X2(n−1)
将项中右侧替换为样本方差S^2,得
σ2n−1S2∼X2(n−1)(4)
即样本方差乘以总体方差分之样本数-1服从样本数减一的卡方分布
易知样本方差为
S2=n−11i=1∑n(Xi−X)2
注意这里的 S^2 仍为一个随机变量,因为没有代入具体的值
E(S2)=σ2(5)
即样本方差的期望为总体方差,这很合理
最后一个结论,样本均值和样本方差相互独立
X⊥S2(6)
上述(1)(2)(3)(4)(5)(6)式为常考的六个结论