随机变量的数字特征

离散随机变量数学特征

数学期望

一维离散随机变量得数学期望定义：数学期望即所有值乘以其发生概率之和

$$E=\sum_{i=0}^n P(i)Value(i)$$

其中P(i)为概率；Value(i)为值

统计意义：反映了随机变量所有取值的中心位置

性质

• 对于常数 c，E(c) = c，因为默认常数概率为 1，故 E(c) = 1xc = c
• 对于随机变量 X，E(cX) = cE(X)，其中 C 为常数

对于随机变量函数f，在得到概率分布表后按照同一步骤（即值、概率相乘求和）求出数学期望

举个栗子

抓住代价：在这里是检测数量，方案一固定为100次，方案二不固定，五人一检，阳性则每人依次检测，阴性则略过

明确取值：在方案二中，每组检测次数取值可能为1或6，根据题目已给条件求出各自概率，再按比例扩大范围

这里有一个分组的问题，一开始没想到

方差和标准差

方差：差距的平方的期望

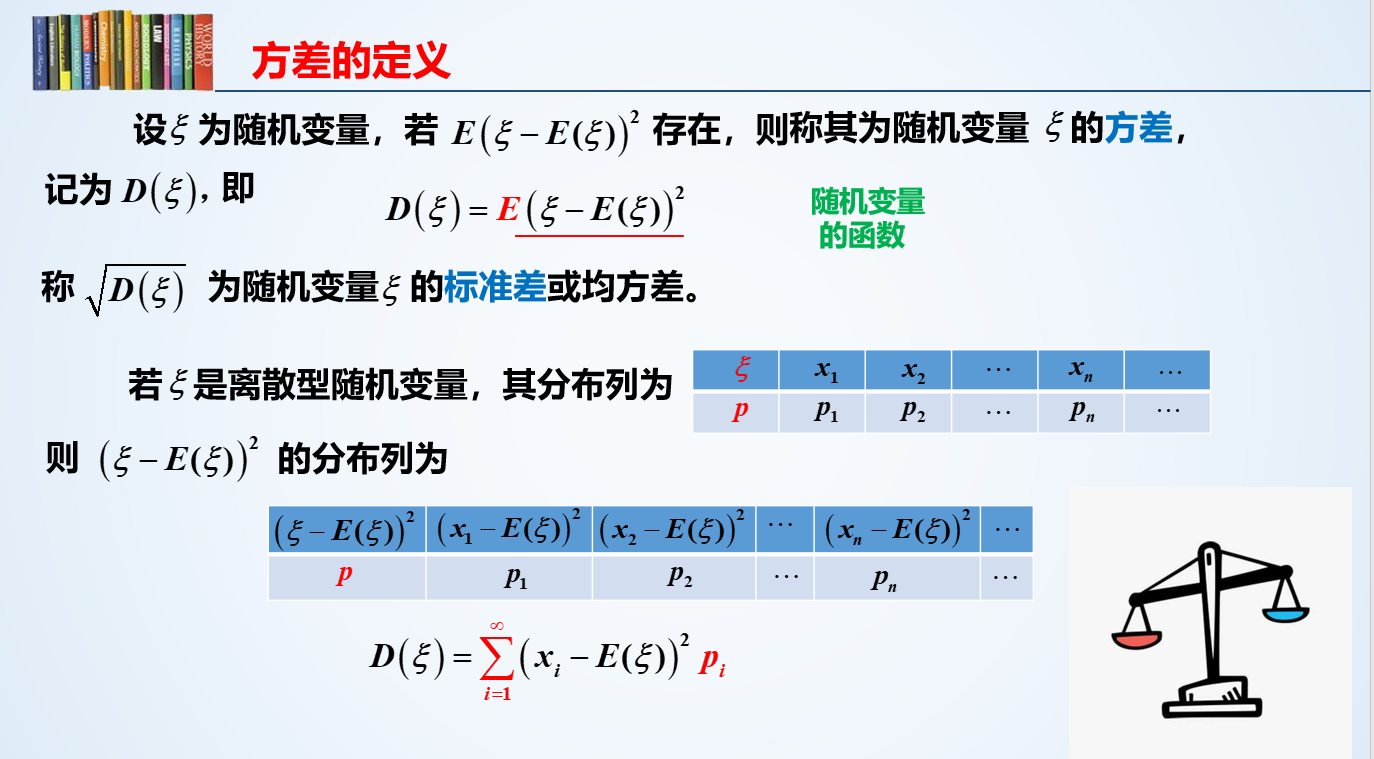
• 方差开根即为标准差

• 先求出一维概率分布的数学期望，用(xi-期望)的平方作为新的值，xi的概率作为这个值的概率，组成一个新的一维概率分布

  这个新概率分布的数学期望即为原概率的方差，记为D(X)

方差体现了随机变量围绕期望的偏离程度，方差越小，说明分布越集中，越大说明分布越分散（常用于判断产品优劣）

性质

• 常数的方差为0，即D(c) = 0，毫不偏差（常数拥有概率为1，偏差为0的特点）
• D(cX) = c²D(X)，常数开出来要平方
• D(X+Y) = D(X)+D(Y)，和变量的方差等于变量的方差和，前提是变量X,Y相互独立

常见概率分布的方差

分布	参数	数学期望	方差
两点分布	0<p<1	p	p(1-p)
二项分布	n>=1, 0<p<1	np	np(1-p)
泊松分布	λ>0	λ	λ
几何分布	0<p<1	1/p	(1-p)/p²

随机变量函数的数学期望

对于一维随机变量 X，已知

X	-2	0	1	3
P	1/3	1/2	1/12	1/12

$$\begin{aligned} E(2X^2+5)&=((-2)^2\times2+5)\times\frac{1}{3}+(0+5)\times\frac{1}{2}+(1\times2+5)\times\frac{1}{12}+(3^2\times2+5)\times\frac{1}{12}\\\\ &=\frac{13}{3}+\frac{5}{2}+\frac{7}{12}+\frac{23}{12}=\frac{28}{3} \end{aligned}$$

对于二维随机变量 X/Y，已知

X/Y	0	1
0	(1-p)^2	p(1-p)
1	p(1-p)	p^2

求得E(X+Y)，将f(X+Y)的概率分布表列出，用一维的办法解即可

f	0	1	2
P	(1-p)^2	2p(1-p)	p^2

连续随机变量数字特征

数学期望

回忆以下离散型随机变量的数学期望：概率和值的乘积的和

连续型随机变量的数学期望

$$\int_{-∞}^{+∞} xp(x)dx$$

即对xp(x)在实数范围内积分，这很合理，就是值*概率的和，若该积分不为正无穷，则称离散型随机变量数学期望存在，为这个积分结果

常见连续型随机变量的数学期望：

1、均匀分布X~U(a,b)的数学期望为(a+b)/2（区间中间）

2、指数分布

$$p(x)=\lambda e^{-\lambda x}, x>0 \rightarrow E(X) = \frac{1}{\lambda}$$

3、正态分布X~N(u,v^2)

$$p(x)=\frac{1}{\sqrt{2\pi}v}e^{-\frac{(x-u)^2}{2v^2}} \rightarrow E(X) = u$$

连续型随机变量函数的数学期望：

对于普通函数f(x)，将其自变量换为一个连续型随机变量Z，那么f(Z)的数学期望为：∫(-∞,+∞) f(x)p(x)dx

• 只改变值，概率不变，所以只将积分项中x换为f(x)

二维连续型随机变量函数的数学期望：

性质：基本与离散型随机变量期望性质一致

• 当随机变量取值有限，必有期望，且期望大于下限小于上线
• 常数的期望为常数自身
• E(k1X+k2Y) = k1*E(X)+k2*E(Y)，其中k1,k1为实数，X,Y为连续型随机变量
• 若连续型随机变量X,Y相互独立，则E(XY) = E(X)E(Y)

方差

计算：D(X)=E((X-EX)^2)

在这里构造一个函数：

$$f(x)=[x-E(X)]^2$$

用求连续型随机变量函数的方法求方差

即

$$D(x) = \int_{-∞}^{+∞} (x-E(X))^2\times p(x)dx$$

化简可得

$$D(x) = E(X^2)-E(X)^2 = ∫_{-∞}^{+∞} x^2p(x)dx - [∫_{-∞}^{+∞} xp(x)dx]^2$$

常见连续型随机变量的方差

分布	参数	期望	方差
两点分布	0<p<1	p	p(1-p)
二项分布	n>=1,0<p<1	np	np(1-p)
泊松分布	λ>0	λ	λ
几何分布	0<p<1	1/p	(1-p)/p^2
均匀分布	a<b	(a+b)/2	(b-a)^2/12
指数分布	λ>0	1/λ	1/λ^2
正态分布	u,v>0	u	v^2

性质

• 常数的方差为0
• D(cX) = c^2 D(X)
• 对于相互独立的随机变量X,Y，D(X+Y) = D(X)+D(Y)

切比雪夫不等式

之前也提到过，方差越大，一般来说数据离期望会较远，方差越小则反之

切比雪夫不等式使用严格的数学公式规范这种直觉，设随机变量X期望为E(X)=u，方差D(X)存在，则

$$P(|X-u|\geq ε)\leq \frac{D(X)}{ε^2}\quad\quad P(|X-u|<ε)\geq 1-\frac{D(X)}{ε^2}$$

其中ε为任意正数

协方差与相关系数

对于二维随机变量(u,v)，协方差反应u,v之间的联系

定义协方差为

$$Cov(u,v) = E[(u-Eu)(v-Ev)]$$

展开计算可得

$$Cov(u,v) = E(uv)-E(u)E(v)$$

性质

• 交换律：Cov(u,v) = Cov(v,u)

• 数乘：Cov(au,bv) = abCov(u,v)

• 分配律：Cov(u1+u2,v) = Cov(u1,v)+Cov(u2,v)

• 和方差的关系：D(u+v) = D(u)+2Cov(u,v)+D(v)，当u,v独立时，Cov(u,v)=0，自然D(u+v)=D(u)+D(v)

相关系数

$$\rho = \frac{Cov(u,v)}{\sqrt{(Du)(Dv)}}$$

• 相关系数是随机变量间线性关系强弱的一个量度，当|p|越大，两随机变量线性关系较密切，|p|越小，线性相关程度较差，当p=0，二者线性无关
• 值域为[-1,1]
• 当p=1，两个随机变量正线性相关，当p=-1，二者负线性相关

协方差也可以表示为

$$Cov(u,v) = \rho\,\sqrt{D(u)D(v)}$$

变量和的方差可以表示为

$$D(u+v) = D(u) + 2\rho\,\sqrt{D(u)D(v)} + D(v)$$

当线性无关，即

$$p=0 \rightarrow Cov(u,v)=0, D(u+v)=D(u)+D(v)$$

注意，独立一定线性无关，但线性无关不一定相互独立，二者是两个不同的概念