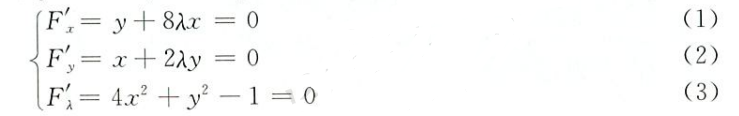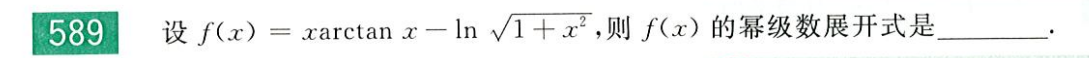求解微分方程常忘方法

一阶微分的倒置求解

T79

就是把 dy/dx 转化为 dx/dy，从而使其变成一个可分离变量的微分方程，简化运算，最后倒过来就行

全微分方程的不变性

T90、93

原理就是二阶偏导相同（此时偏导均连续）

二阶非齐次微分方程

非齐次解的形式

$$y^* = x^ke^{ax}Q_m(x)$$

通解

$$(C_1+C_2x)e^{rx}\quad C_1e^{r_1x}+C_2e^{r_2x}$$

常见二重积分

非中心圆域极坐标化

一些非规则圆域的 r 上限的判定，非常不会，T110、112

非中心区域的重积分对极坐标的转换，如

$$D = \{(x,y)|(x-1)^2+(y-1)^2\leq 4\}$$

一个以 (1,1) 为圆心，以 2 为半径的圆域，则令

$$x = rcos\theta + 1\quad y = rsin\theta + 1$$

这样将圆心手动移动到原点，关于 D 的积分可化为

$$\iint_{D}f(x,y)dxdy = \int_0^{2\pi}\theta\int_0^2f(rcos\theta+1,rsin\theta+1)rdr$$

如

对于圆域

$$(x-\frac{1}{2})^2+y^2 \leq \frac{1}{4}$$

设

$$\begin{cases} x = rcos\theta+\frac{1}{2}\\ y = rsin\theta \end{cases}$$

其对应的极坐标积分即为

$$\int_0^{2\pi}\theta\int_0^{\frac{1}{2}}r(rcos\theta+\frac{1}{2})(rsin\theta)dr$$

可以轻易得到结果，将积分的限简化了，但复杂化了被积函数

对称区间化简

涉及区间的压缩，和两个变量的转化

原批函数

二元微分定义相关

二重积分定义的理解

对于极限

$$\lim_{n\rightarrow\infty}\int_1^{\frac{1}{2n}}e^{-y^2}dy+\int_1^{\frac{3}{2n}}e^{-y^2}dy+...+\int_1^{\frac{2n-1}{2n}}e^{-y^2}dy$$

其实等价于一个二重积分

$$\int_0^1dx\int_1^xe^{-y^2}dy$$

通过交换次序积分可求解得为

$$\frac{1}{2}(\frac{1}{e}-1)$$

这个极限怎么求得？

$$\lim_{n\rightarrow\infty}\frac{2^{\frac{1}{n}}-1}{(2n+1)^{\frac{1}{n}}} = ln2$$

偏导的定义求法

一定要分清楚是谁趋近于 0，是变化的 x 量趋于 0

f(x, y) 在 (0, 0) 点在 x 方向上的偏导

$$f'_x(0,0) = \lim_{x\rightarrow0,y=0}\frac{f(x,0)-f(0,0)}{x}$$

f(x, y) 在 (x0, 0) 点在 x 方向上的偏导

$$f'_x(x_0,0) = \lim_{x\rightarrow0,y=0}\frac{f(x_0+x,0)-f(x_0,0)}{x}$$

f(x, y) 在 (x0, y0) 点在 x 方向上的偏导

$$f'_x(x_0,y_0) = \lim_{x\rightarrow0,y=y_0}\frac{f(x_0+x,y_0)-f(x_0,y_0)}{x}$$

连续、可偏导、可微和偏导连续

偏导连续一定可微（反之不成立），可微一定可偏导（反之不成立），可偏导不一定连续，连续不一定可偏导

f(x, y) 在 (0, 0) 处连续

$$\lim_{x\rightarrow0,y=g(x)}f(x,y) = f(0,0)$$

f(x, y) 在 (0, 0) 可偏导：原函数可偏导，不一定有原函数连续，不是一个维度的问题

$$f'_x(0,0) = \lim_{x\rightarrow0,y=0}\frac{f(x,0)-f(0,0)}{x}\,存在$$

f(x, y) 在 (0, 0) 处可微：可微一定可偏导，也一定连续

$$\lim_{x\rightarrow0,y\rightarrow0}\frac{f(x,y)-f(0,0)-f'_x(0,0)x-f'_y(0,0)y}{\sqrt{x^2+y^2}}\,存在$$

偏导连续的判定，首先要求出偏导（偏导连续一定有原函数可微，优先级最高）

$$f'_x(x,y) = \frac{∂f}{∂x}$$

然后对这个新的二元函数进行连续性的判定，和 f(x, y) 的连续性判定一样，如若偏导在 (0, 0) 点连续，则有

$$\lim_{x\rightarrow0,y=g(x)}f'_x(x,y) = f'_x(0,0)$$

注意这里有一些奇形怪状的函数，如

$$f'_x(x,0)\quad f'_y(1,y)$$

这些都是基于偏导，固定了一个维度变量的一元函数，这个一元函数连续只能证明偏导在单个维度的某一个值上连续，无法证明偏导连续，自然不能证明原函数可微

自然，可微也不能证明偏导连续，更不能证明这些奇形怪状的一原函数连续，即这些一元函数和可微之间的证明既不充分也不必要

另外，当偏导连续，有

$$\frac{∂^2f}{∂x∂y} = \frac{∂^2f}{∂y∂x}$$

添加一个偏连续的概念，做题做到了，二元方程 f(x, y) 在 (x0, y0) 点对 x 偏连续，指

$$\lim_{x\rightarrow x_0}f(x, y_0) = f(x_0, y_0)$$

同理对 y 偏连续，即有

$$\lim_{y\rightarrow y_0}f(x_0, y) = f(x_0, y_0)$$

值得注意的是，可偏导一定偏连续，偏连续不一定可偏导

和上面求偏导的思想是一样的，都是通过确定另一个自变量，将二元函数实际上转化为一个一元函数，再对这个一元函数求导

$$f'_x(x_0,y_0) = \lim_{x\rightarrow x_0}\frac{f(x, y_0)-f(x_0,y_0)}{x}$$

喏，这里完全就是把 y 的值固定为 y0，原二元函数名存实亡，降为一个一元函数 f(x, y0)，再对这个一元函数求导，即为偏导

二元函数驻点、极值点和条件极值

驻点和极值点关系

首先明确一点，在二元函数中，是驻点不一定是极值点（和一元函数保持一致），并且，是极值点不一定是驻点，这是因为在极值点有可能不可偏导，如

$$f(x,y) = |x|+|y|$$

显然，根据定义，f 在 (0, 0) 点取极小值，但两个偏导在该点均左右导数不等，即不可偏导，更不用说偏导为零是一个驻点了

自然的，当 f 取极值，更不可能推出其对应一元函数在该点取极值（因为很有可能这个一元函数压根就不可导）

另外还有一嘴，即使 (x0, y0) 对于 f(x, y) 在区间 D 内是唯一的极大值点，也不能说 f(x, y) 在 D 内的最大值是 f(x0, y0)，原因未知？？？

判断极值点

一般情况下，要你判断是否是极值点，首先还是要求偏导的，就是把两个偏导先求出来，这种题一般都求的出来

如果求不出偏导，就要从定义上考虑该点是否是极值点

第一步：一定是判断所求点的偏导是否均为 0，若不为 0，一定不是极值点，否则继续判断

$$\frac{∂f}{∂x}_{|(x_0,y_0)} = \frac{∂f}{∂y}_{|(x_0,y_0)} = 0$$

第二步：当偏导均为 0 后，对原函数求二次偏导，并设

$$A = \frac{∂^2f}{∂x^2}_{|(x_0,y_0)}\quad C = \frac{∂^2f}{∂y^2}_{|(x_0,y_0)}\quad B = \frac{∂^2f}{∂x∂y}_{|(x_0,y_0)}$$

第三步：对这三个二重偏导进行大小判定，若

$$AC - B^2 \leq 0$$

则并非极值点，否则，极值点存在，即此时有

$$AC-B^2 > 0$$

第四步：判断 A 的大小

$$A > 0\Rightarrow f(x_0,y_0)为极小值\\ A < 0\Rightarrow f(x_0,y_0)为极大值$$

注意，这里不存在 A = 0 的情况，因为这样的话第三步的判定一定 < 0，极值直接就不存在了

条件极值

通过引入第三变量 λ 的方式来求条件极值，如对于

$$f(x,y) = 1+x+y\quad (x,y)\in\{x^2+y^2\leq1\}$$

引入一个变量 λ 将条件引入函数，构造

$$F(x,y,\lambda) = 1+x+y+\lambda(x^2+y^2-1)$$

通过对这个新函数求偏导，令为 0，求得极值点，从而得到条件极值

最值求解

660 给的求解程序

求有限区间内求最值，其实就是在极值的基础上，求所有驻点的函数值以及边界函数值，最后做一个比较而已

等价于求解 g(x, y) = xy 在 D 上的最小值

$$F(x,y,\lambda) = -xy + \lambda(4x^2+y^2-1)$$

求偏导有

我在第一次求解时，用到基本不等式

$$(2x+y)^2 = 4x^2+y^2+4xy\geq0$$

左右移项除以 4 得

$$-xy\leq \frac{4x^2+y^2}{4}$$

又由题意知

$$4x^2+y^2 \leq 1$$

固有

$$-xy \leq \frac{1}{4}$$

自然函数 f(x, y) 得最大值为

$$e^{\frac{1}{4}}$$

再举一个栗子，稍简单点，但一定注意要比较边界值

无穷级数

判敛

比、商、根

• 条件收敛的条件：一般项单调递减且极限趋于 0
• 绝对收敛一定条件收敛，条件发散一定绝对发散

几何级数（几何级数）的判敛

当指数严格小于 1 时，才收敛

有一个小技巧，我不知道对不对，就是对于某个级数，比如

$$I = \sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}$$

已知这是一个交错收敛级数，且当 n 趋于无穷时，有

$$\lim_{n\rightarrow\infty}\frac{a_{n+1}}{a_n}=1$$

此时对他复合一个式子 bn，原级数变为

$$I' = \sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}b_n$$

当 n 趋于无穷时，当这个 bn 趋于 0，则原级数 I 更加收敛，I' 将变为绝对收敛，而当 bn 趋于常数时，原级数收敛性不变，I' 仍为条件收敛

对于一般项 an，若其已经极限趋于 0 且单调递减，判断其是否绝对收敛，可以考虑他的一个必要条件

$$a_n'=\frac{da_n}{dn}=0$$

即对一般项的无穷点求导，若绝对收敛这个导函数必须等于 0

积分判敛法：nmsl

计算收敛半径

商，代入 x 幂的未知数计算，收敛半径即为

$$|\frac{a_{n+1}x^{n+1}}{a_nx^n}|<1\rightarrow\rho=|\frac{a_{n+1}}{a_n}|\quad R = \frac{1}{\rho}$$

对于临界值，需要直接代入幂级数，对这个既定的无穷级数进行判敛，若收敛则为闭区间，否则为开区间

和函数和幂级数

和函数，就是幂级数的值，这个值是一个关于自变量 x 的函数，又是由级数求和得到，所以叫做和函数

和函数通过泰勒展开可以得到幂级数，幂级数通过收束（消去系数 n）得到和函数

通过微分方程求解和函数，找到和函数和其一阶、二阶导数之间的数量关系，建立微分方程求解

$$S'(x)=-xS(x)\rightarrow y' = -xy$$

可分离变量微分方程求解，并且易知 S(0) = 1

$$S''(x) = S(x)\rightarrow y''-y=0$$

根据特征值 1/-1 列出二阶齐次通解，且有S(0) = 0, S'(0) = 1

常见的三个麦克劳林展开

1. $$\frac{1}{1-x}=1+x+x^2+...+x^n=\sum_{n=0}^\infty\ x^n$$
2. $$\frac{1}{1+x}=1-x+x^2+...+(-1)^{n}x^n=\sum_{n=0}^\infty\ (-1)^nx^n$$
3. $$ln(1+x) = x-\frac{x^2}{2}+...+(-1)^{n-1}\frac{x^n}{n}=\sum_{n=1}^\infty\frac{(-1)^{n-1}x^n}{n}$$
4. $$-ln(1-x) = x+\frac{x^2}{2}+...+\frac{x^n}{n}=\sum_{n=1}^\infty\frac{x^n}{n}$$

牢记，分式展开系数均为 1/-1，1/(1-x) 各项均为正，1/(1+x) 展开为交替级数，ln(1+x) 的泰勒展开交替且每项均除以 n，-ln(1-x) 各项均为正

对于反三角函数的幂级数求解，通过其导函数的幂级数积分得到

$$arctanx-0=\int_0^x\frac{dx}{1+x^2}=\sum_{n=0}^{\infty}(-1)^n\int_0^xx^{2n}dx=\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}$$

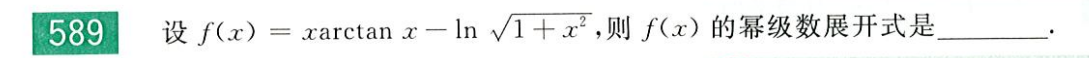
这里还涉及到一个幂级数合并的问题

• 首先把幂级数的起始位置统一，如这里都从 n = 0 开始求和
• 统一过程中要注意正负号的变化和 x 的指数的变化

通过泰勒幂级数求和函数

泰勒展开求导数

对于 f(x)，直接展开，有

$$\begin{aligned} f(x)=&\frac{1}{x^2}(\frac{x^2}{2!}-\frac{x^4}{4}+\frac{x^6}{6!}+...)\\ =&\frac{1}{2}-\frac{x^2}{4!}+\frac{x^4}{6!}-\frac{x^6}{8!}+o(x^6) \end{aligned}$$

所以求 6 阶导，x^6 所在项会变为常数，其之前均导为 0，其之后均导为带 x 的项，当 x=0 均取 0，故

$$f^{(6)}(0)=-\frac{6!}{8!}=-\frac{1}{56}$$

选 D

傅里叶级数

傅里叶级数的系数

$$a_n=\frac{1}{l}\int_{-l}^lf(x)cos(n\pi x)dx\quad b_n=\frac{1}{l}\int_{-l}^lf(x)sin(n\pi x)dx$$

重积分、曲线曲面积分

三重积分，先二重积分，再单积分

曲线积分：积分区域是一条曲线

第一类曲线积分

利用奇偶性和对称性简化运算

第二类曲线积分