离散对数和椭圆曲线

阶和原根

阶和原根的定义

若对于数 a，有

$$a^d\equiv1\,mod\,m$$

且 d 是满足上述方程的最小正整数，则 d 为整数 a 模上 m 的阶，记作

$$ord_m(a) = d\quad\quad\sigma_m(a) = d$$

寻找整数 a 模上 m 的阶

int step(int a, int m){
    // φ(m) 为 m 的欧拉函数值
    for(int i = 1; i < φ(m); i++){
        if(pow(a, i) % m == 1){
            return i;
        }
    }
    return φ(m); // 若执行到这，也说明 a 是 m 的一个原根
}

由欧拉定理可知，当(a, m) = 1时，下式一定成立

$$a^{φ(m)}\equiv1\,mod\,m$$

当 a 模上 m 的阶 ord(a) = d，这个阶 d 等于 m 的欧拉函数值 φ(m) 时，我们称 a 是模 m 的一个原根

由于欧拉定理的前提条件(a, m) = 1，故原根 a 只有可能出现在 m 的简化剩余系中（也叫既约剩余系，其元素个数等于 φ(m)）

阶和原根的性质

阶将整除使同余方程成立的任意指数

$$ord_m(a)=d\rightarrow a^{d_i}\equiv1\,mod\,m\quad d\mid d_i$$

换句话说，阶 d 一定是其余所有使指数同余方程成立的指数 di 的因子（最小公因子）

剩余系的原根表示

用原根的指数形式可以表示模 m 的一个既约剩余系

$$[1,a,a^2,...,a^{φ(m)-1}]$$

若 m 是一个素数，原根可以表示一整个剩余系，即完全剩余系

$$[0,1,a,a^2,...,a^{φ(m)-1}]$$

对于原根的指数，有以下推论，当 a 是模 m 的原根，则 a 的 k 次方也是模 m 的原根

$$a^k\equiv1\,mod\,m\quad (k,φ(m))=1$$

其实这是模 m 因子运算的一个子集，完整的推论是说，当

$$(k,φ(m)) = d\rightarrow a^{\frac{φ(m)}{d}}\equiv1\,mod\,m$$

d 是模 m 的某个因子，k 是原根上要指的指数，并且这个 k 一定是 a 模 m 的阶（当 d = 1 时，a 的指数 φ(m)/d 则一定等于 φ(m)，即 φ(m) 为 a 的阶，故 a 为原根）

求解阶和原根

求解原根：最朴素的想法就是从小往上遍历，再一个个指数从小往大遍历，找到第一个 d = ord(a) 的整数

但根据原根 a 的性质

$$(k,φ(m)) = d\rightarrow a^k\equiv1\,mod\,m$$

可以根据已知的某一个快速求解所有原根

求解所有的阶

快速求解单一原根，根据 φ(m) 的因子指数计算，如求解 43 的一个原根，有

$$φ(43) = 42\rightarrow[1,2,3,6,7,14,21,42]$$

在对原根进行判断时，不用一个一个往上爬着求，直接求因子次方即可，如

$$2^2\equiv4\quad2^3\equiv8\quad2^6\equiv21\quad2^7\equiv-1\quad 2^{14}\equiv1\,(mod\,43)$$

故 2 的阶为 14，不等于 φ(m)，故不是原根，对于 3

$$3^2\equiv9\quad...\quad3^{42}\equiv1\,(mod\,43)$$

故 3 是 43 的一个原根，再根据既约剩余系的指数 i

$$[1,3,3^2,...,3^{41}]$$

若有指数 i 与 φ(m) 互质

$$(i, φ(m)) = 1\rightarrow (3^{i})^{φ(m)}\equiv1\,mod\,43$$

则 3 的 i 次方的阶为 φ(m)，一定也为原根

如对于指数 5 而言，其与 φ(m) 互质（最大公因子为 1）

$$(5,42)=1\rightarrow 3^5 \equiv 28\,mod\,43$$

所以 28 也是 43 的一个原根

离散对数密钥协商

DH（Diffie-Hellman 算法），即为密钥协商

双方密钥协商过程如下

1. 首先，选取一个大素数模 p，以及它的一个原根 g
2. A 生成一个随机数 x，发送 g 的 x 次方给 B
3. B 收到 g 的 x 方，另外生成一个随机数 y，并发送给 A

此时 A 和 B 就通过

$$g^{xy}$$

作为会话密钥进行加密解密，即设 a 为明文

$$c \equiv g^{xya}\,mod\,p\quad a =ind_gc$$

a 为模 p 关于原根 g 的 c 的离散对数

椭圆曲线

群论基础

群、子群、阿尔贝群、陪集

• 封闭性
• 结合律
• 单位元
• 逆元
• 交换律

自己去看，和离散数学内容重合

椭圆域几何定义及倍点

狭义的椭圆曲线

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

广义的椭圆曲线

$$y^2=x^3+ax+b$$

每个椭圆曲线都有一个无穷远点 O，这是椭圆曲线上的加法单位元，其实就是纵坐标 y = 0 的点

同一直线上的三个不同点的和一定为 O，单位元点有以下性质（符合群的定义）

• O + O = O
• P + O = P

椭圆上的加法：图 a 中，Q+R = -P1，P1 为直线 QR 和椭圆曲线的交点，-P1 为其关于 x 轴的对称点，图 b 同理

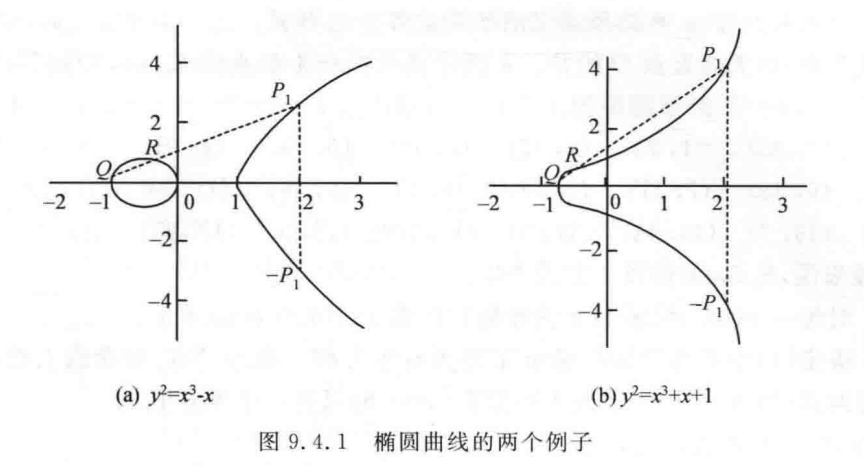
关于倍点，倍点运算即为重复加法运算

• 对于 2Q = Q+Q 来说，即在椭圆曲线一上做 Q 点的切线，假设与椭圆曲线二交于 R，则 -R 为其和点
• 对于 3Q = Q+Q+Q 而言，已知 2Q = -R，再加一个 Q，即连接 Q 和 -R，其交点 H 一定过曲线一，-H 即为 3Q

注意这里的 -R 和 -H 均为椭圆曲线上的逆元，其实并非直接将纵坐标取负（只是在上述两图中如此，为特殊情况），下面有说，其实是纵坐标的负数模上椭圆系的系数

椭圆域的代数加法

一些概念

• 椭圆域：即椭圆曲线上的阿尔贝群（满足交换律的群）
• 椭圆离散系，去除线的概念，椭圆系由一个个离散的点组成

椭圆曲线的代数逆元

$$P(x,y)\rightarrow P^{-1}=(x,\,-y\,mod\,p)$$

其中 p 为椭圆曲线的参数，有时也直接记作 -P

当某点的纵坐标 y 被 p 整除时，我们说这个点是一个无穷远点 O，如对于系数 p = 23 的椭圆域一定有无穷远点 O 如下

$$E_{23}(a,b)\rightarrow O(x_0, 23n)$$

在代数上，加法的坐标满足：P(x1, y2), Q(x2, y2), R(x3, y3) = P + Q

$$\begin{cases} x_3=k^2-x_1-x_2(mod\,p)\\ y_3=k(x_1-x_3)-y_1(mod\,p) \end{cases}$$

对于常数 k，有

$$k= \begin{cases} \frac{3x_1^2+a}{2y_1}\,(mod\,p)&P=Q\\ \frac{y_2-y_1}{x_2-x_1}\,(mod\,p)&P\neq Q \end{cases}$$

其中 a 是椭圆曲线中 x 的系数（这里的 a 和 p 都是定义椭圆域的常数，已知）

椭圆曲线中逆元的计算（如何将小数化为整数），如对于 E23 的椭圆域

$$-2^{-1}\,mod\,23=\,?$$

首先要将 2 的 -1 次方视为 2 的逆元，根据辗转相除法可知

$$1 = 23-11\times 2\Rightarrow 2^{-1}=-11=12\,(mod\,23)$$

所以有

$$-2^{-1}\,mod\,23=-12\,mod\,23=11$$

举个栗子：在系数在E23上且a = 1的椭圆系中，有P(3, 10), Q(9, 7)

1、求解 -P

根据椭圆系的逆元定义，有

$$-P=(3,-10\,mod\,23)=(3,13)$$

2、求解 R = P + Q

首先明确 P 不等于 Q，则斜率 k 为

$$k = \frac{y_2-y_1}{x_2-x_1} = -2^{-1}\,mod\,23$$

这里采用逆元的计算方式来表示 -1/2，根据广义欧几里得有

$$1 = 23-11\times2$$

固有

$$2^{-1} = -11\Rightarrow k = -2^{-1}=11\,mod\,23$$

根据公式直接计算 R 的横坐标

$$x_3 = k^2-x_1-x_2=121-3-9\,(mod\,23)=17$$

纵坐标

$$y_3 = k(x_1-x_3)-y_1=11\times(3-17)-10\,(mod\,23)=20$$

故 R 坐标为 (17, 20)

3、求解 2P

这是一个倍点运算，此时斜率 k 为

$$k = \frac{3x_1^2+a}{2y_1}=\frac{3\times3^2+1}{20}=\frac{7}{5}=7\times5^{-1}$$

根据辗转相除法，易知 5 的逆元为 -9

$$\begin{aligned} 23 &= 4\times5+3\\ 5 &= 3+2\\ 3 &= 3+1 \end{aligned} \Rightarrow \begin{aligned} &= -5+2\times(23-4\times5)=2\times23-9\times5\\ &= 3-(5-3)=-5+2\times3\\ 1 &= 3-2 \end{aligned}$$

则有

$$k = 7\times(-9)\,mod\,23=-63\,mod\,23=6$$

代入坐标计算公式

$$\begin{aligned} x_3&=k^2-2x_1\,(mod\,23)=7\\ y_3&=k(x_1-x_3)-y_1\,(mod\,23)=12 \end{aligned}$$

故 2P 坐标为 (7, 12)

椭圆域的倍点运算

对于 nP，将系数 n 用二进制表示，采用和快速模运算类似的方式，对 P 进行 logn 次加法（二倍点）运算

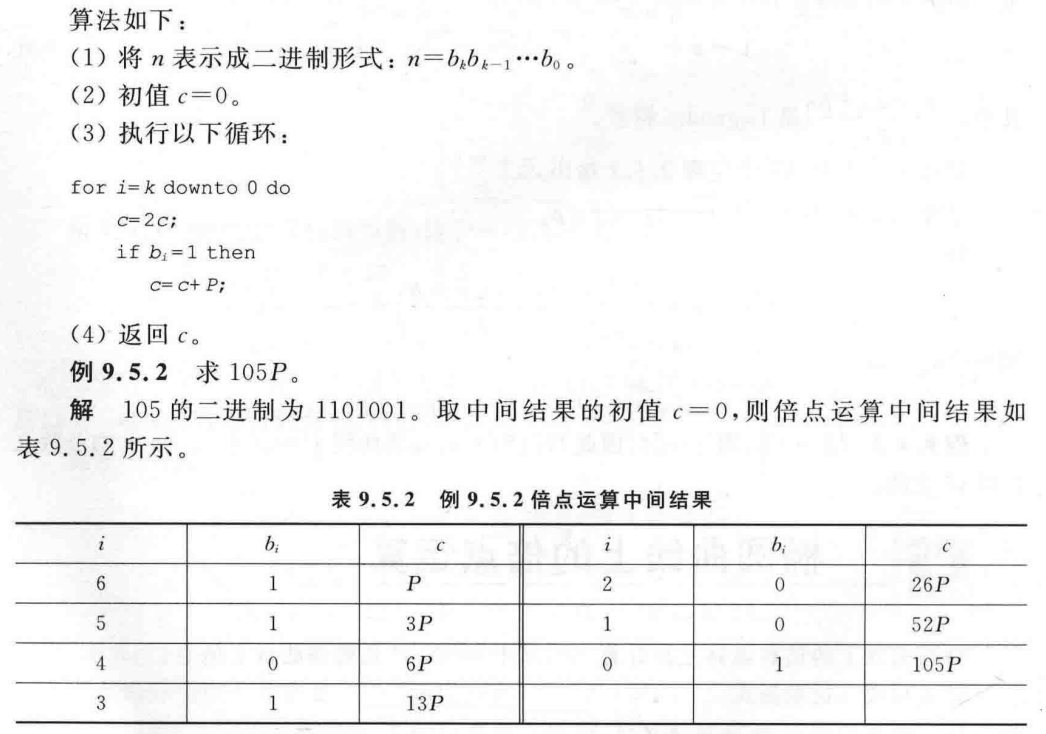
就是当当前位为 1 时，多加一个原点 P，同时每一轮进行一次二倍点运算（乘以 2）

• 模平方运算是当当前位为 1 时多乘上一个底数 a，其余时间每轮进行平方运算

倍点运算的代码实现

椭圆曲线加密

加密解密过程（背下来），公钥是用来加密的，私钥是用来解密的

就是通过一个公钥，进行倍点运算加密，倍点运算结果很难进行还原