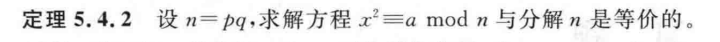一次同余方程 方程形式
a x ≡ b m o d m
ax \equiv b\,mod\,m
a x ≡ b m o d m
无解条件 有解的判定条件,对于一次方程
a x ≡ b m o d m
ax\equiv b\,mod\,m
a x ≡ b m o d m ( a , m ) ∣ b
(a, m)\mid b
( a , m ) ∣ b (a, m)
如对于
32 x ≡ 12 m o d 8
32x\equiv 12\,mod\,8
32 x ≡ 12 m o d 8 ( 32 , 8 ) = 8 ∤ 12
(32,8) = 8\nmid 12
( 32 , 8 ) = 8 ∤ 12
穷举剩余类求解 即求解模 m 余 b 的 x 值,已知这个 x 一定存在于模 m 的一个完全剩余系中,采用穷举法一个个代入可以得到 x 的取值
list solve_congruential_equation ( int a, int b, int m) {
list res;
for ( int x = 0 ; x < m; x++ ) {
if ( ( a* x) % m == b) {
res. add ( x) ;
}
}
return res;
}
1 2 3 4 5 6 7 8 9 10 11 12
手动计算时,采用这样的步骤
算出系数和模数的最大公因子,整除余数,判定有解 从 0 开始,从小到大遍历模数 m 的剩余类,找到最小的一个 x 值,记为 x0 则有通解
x = x 0 + t m ( a , m ) t ∈ [ 0 , ( a , m ) )
x = x_0+t\frac{m}{(a,m)}\quad t\in[\,0, (a,m)\,)
x = x 0 + t ( a , m ) m t ∈ [ 0 , ( a , m ) ) 6 x ≡ 2 m o d 8
6x\equiv2\,mod\,8
6 x ≡ 2 m o d 8 (a, m) = (6, 8) = 2,由于2 | 2,所以该方程有解且有两个解
从小到大遍历 8 的剩余类,0, 1, 2, 3,发现
6 × 3 ≡ 2 m o d 8
6\times3\equiv 2\,mod\,8
6 × 3 ≡ 2 m o d 8 x = x 0 + t m ( a , m ) = 3 + 4 t t ∈ [ 0 , 2 )
x = x_0+t\frac{m}{(a,m)} = 3+4t\quad t\in[0, 2)
x = x 0 + t ( a , m ) m = 3 + 4 t t ∈ [ 0 , 2 ) x1 = 3, x2 = 7
逆元求解互素的系数和模方程 对于系数和模数互素的一元线性同余方程
a x ≡ b m o d m ( a , m ) = 1
ax \equiv b\,mod\,m \quad (a,m) = 1
a x ≡ b m o d m ( a , m ) = 1 x ≡ a − 1 b m o d m
x\equiv a^{-1}b\,mod\,m
x ≡ a − 1 b m o d m 2 x ≡ 3 m o d 7 1 = 7 − 3 × 2
2x\equiv 3\,mod\,7\quad 1=7-3\times2
2 x ≡ 3 m o d 7 1 = 7 − 3 × 2 1 = 2 × 4 − 7
1 = 2\times4-7
1 = 2 × 4 − 7 x = 4 × 3 m o d 7 = 5
x = 4\times3\,mod\,7 = 5
x = 4 × 3 m o d 7 = 5 60 x ≡ 7 m o d 37 → ( 37 x + 23 x ) ≡ 7 m o d 37
60x\equiv7\,mod\,37\rightarrow(37x+23x)\equiv7\,mod\,37
60 x ≡ 7 m o d 37 → ( 37 x + 23 x ) ≡ 7 m o d 37 [ ( 37 x m o d 37 ) × ( 23 x m o d 37 ) ] m o d 37 = 1 × ( . . . ) m o d 37
[(37x\,mod\,37)\times(23x\,mod\,37)]\,mod\,37 = 1\times(...)\,mod\,37
[( 37 x m o d 37 ) × ( 23 x m o d 37 )] m o d 37 = 1 × ( ... ) m o d 37 23 x ≡ 7 m o d 37
23x\equiv7\,mod\,37
23 x ≡ 7 m o d 37
RSA 算法 依据一次同余方程进行加密和解密
取两个大素数 p 和 q,计算 n = pxq,作为公钥的一部分
取整数 e 满足
( e , n ) = 1 e ∈ ( 0 , φ ( n ) )
(e,n)=1\quad e\in(0,φ(n))
( e , n ) = 1 e ∈ ( 0 , φ ( n )) c ≡ a e m o d n
c \equiv a^e\,mod\,n
c ≡ a e m o d n a e ≡ c m o d n → a e d = a ≡ c d m o d n
a^{e}\equiv c\,mod\,n\rightarrow a^{ed} = a\equiv c^{d}\,mod\,n
a e ≡ c m o d n → a e d = a ≡ c d m o d n e d ≡ 1 m o d n → e d + n y = 1
ed\equiv1\,mod\,n \rightarrow ed+ny=1
e d ≡ 1 m o d n → e d + n y = 1
通过私钥公钥 e 和模数 n 通过辗转相除法计算 e 的逆元 d 做一个指数模运算,计算明文 a 第一步的算式如下,其中 e 和 n 为已知且必有 (e, n) = 1
e d ≡ 1 m o d n
ed \equiv1\,mod\,n
e d ≡ 1 m o d n a ≡ c d m o d n
a\equiv c^{d}\,mod\,n
a ≡ c d m o d n
孙子定理 数论的内容包括了密码学中的:公钥体制;安全协议
可用于秘密共享、密钥分发与用户认证协议,什么是密钥共享?就比如
A 拥有密钥 1、2 B 拥有密钥 1、3 C 拥有密钥 2、3 只有当至少两个人在场时,即拥有完整的三个密钥,才能进行解密
孙子定理前提条件 用于求解同余方程组
{ x ≡ b 1 m o d m 1 x ≡ b 2 m o d m 2 . . . x ≡ b n m o d m n
\begin{cases}
x\equiv b_1\,mod\,m_1\\
x\equiv b_2\,mod\,m_2\\
...\\
x\equiv b_n\,mod\,m_n
\end{cases}
⎩ ⎨ ⎧ x ≡ b 1 m o d m 1 x ≡ b 2 m o d m 2 ... x ≡ b n m o d m n
{ x ≡ 2 m o d 12 x ≡ 2 m o d 3 → { x ≡ 2 m o d 3 x ≡ 2 m o d 4 x ≡ 2 m o d 3
\begin{cases}
x\equiv 2\,mod\,12\\
x\equiv 2\,mod\,3
\end{cases}
\rightarrow
\begin{cases}
x\equiv 2\,mod\,3\\
x\equiv 2\,mod\,4\\
\cancel{x\equiv 2\,mod\,3}
\end{cases}
{ x ≡ 2 m o d 12 x ≡ 2 m o d 3 → ⎩ ⎨ ⎧ x ≡ 2 m o d 3 x ≡ 2 m o d 4 x ≡ 2 m o d 3 其原理为:由于(4, 3) = 1且3 x 4 = 12,所以有
x ≡ 2 m o d 12 ⟺ { x ≡ 2 m o d 4 x ≡ 2 m o d 3
x\equiv 2\,mod\,12 \iff
\begin{cases}
x\equiv 2\,mod\,4\\
x\equiv 2\,mod\,3
\end{cases}
x ≡ 2 m o d 12 ⟺ { x ≡ 2 m o d 4 x ≡ 2 m o d 3 当求解一次同余方程的时候,也可以通过这种方式简化运算,如
59 x ≡ 27 m o d 91 ⟺ { 59 x ≡ 27 m o d 13 59 x ≡ 27 m o d 7
59x\equiv 27\,mod\,91\iff
\begin{cases}
59x\equiv 27\,mod\,13\\
59x\equiv 27\,mod\,7
\end{cases}
59 x ≡ 27 m o d 91 ⟺ { 59 x ≡ 27 m o d 13 59 x ≡ 27 m o d 7 转化为一个一次同余方程组来进行求解(比直接用逆元运算好算一点)
孙子定理算法 在前提条件满足后,开始该计算程序,对于一次同于方程组
{ x ≡ b 1 m o d m 1 x ≡ b 2 m o d m 2 . . . x ≡ b n m o d m n
\begin{cases}
x\equiv b_1\,mod\,m_1\\
x\equiv b_2\,mod\,m_2\\
...\\
x\equiv b_n\,mod\,m_n
\end{cases}
⎩ ⎨ ⎧ x ≡ b 1 m o d m 1 x ≡ b 2 m o d m 2 ... x ≡ b n m o d m n M = Π m i
M = \Pi\,m_i
M = Π m i M i = M m i
M_i = \frac{M}{m_i}
M i = m i M M i M i − 1 ≡ 1 m o d m i
M_iM_i^{-1}\equiv1\,mod\,m_i
M i M i − 1 ≡ 1 m o d m i x = ∑ i = 1 n b i M i M i − 1 ( m o d M )
x = \sum_{i=1}^nb_iM_iM_i^{-1}\,(mod\,M)
x = i = 1 ∑ n b i M i M i − 1 ( m o d M )
通过扩展欧几里得去掉同余方程组中每个方程的系数 发现模数并不互素,通过模运算的性质展开为多个方程,并删去重复方程 通过孙子定理进行计算求解 x 二次同余 二次剩余 对于二次同余方程
x 2 ≡ a m o d p
x^2\equiv a\,mod\,p
x 2 ≡ a m o d p
欧拉判别法 给定一个二次同余方程,如何判定其是否有解(余数 a 是否是模数 p 的一个二次剩余),采用欧拉判别法,他这样规定
当 p 是一个奇素数且 p 不能整除 a,若
a φ ( p ) 2 ≡ 1 m o d p φ ( p ) = p − 1
a^{\frac{φ(p)}{2}}\equiv1\,mod\,p\quad φ(p) = p-1
a 2 φ ( p ) ≡ 1 m o d p φ ( p ) = p − 1
注意这里的欧拉判别式只有可能余出两种结果,即 1 或 -1,若为 -1,就说明 a 是 p 的二次非剩余
举个栗题:判断下列二次同余方程余数是否是模数的二次剩余
x 2 ≡ 3 m o d 29
x^2\equiv3\,mod\,29
x 2 ≡ 3 m o d 29 3 29 − 1 2 = 3 14 ≡ ? m o d 29
3^{\frac{29-1}{2}} = 3^{14}\equiv\,?\,mod\,29
3 2 29 − 1 = 3 14 ≡ ? m o d 29
i bi c(1) 4 1 c = c x c x a (mod 29) = 33 1 c = c x c x a (mod 29) = 272 1 c = c x c x a (mod 29) = 121 0 c = c x c (mod 29) = 144 mod 29 = 28 = -1
即有
( 3 29 ) = 3 14 m o d 29 = − 1
(\frac{3}{29}) = 3^{14}\,mod\,29=-1
( 29 3 ) = 3 14 m o d 29 = − 1
Legendre 符号 用于表示余数 a 是否是模数 p 的二次剩余,其实这里的判定和欧拉判别一模一样,只是用 Legendre 符号来表示 a 模 p 的逆元
其前提是 p 必须为一个奇素数
( a p ) = { 1 x 2 ≡ a m o d m 有解 − 1 x 2 ≡ a m o d m 无解 0 p ∣ a
(\frac{a}{p}) = \begin{cases}
1&x^2\equiv a\,mod\,m 有解\\
-1&x^2\equiv a\,mod\,m 无解\\
0&p|a
\end{cases}
( p a ) = ⎩ ⎨ ⎧ 1 − 1 0 x 2 ≡ a m o d m 有解 x 2 ≡ a m o d m 无解 p ∣ a ( a p ) = ( a 1 p ) × . . . × ( a n p )
(\frac{a}{p}) = (\frac{a_1}{p})\times...\times(\frac{a_n}{p})
( p a ) = ( p a 1 ) × ... × ( p a n ) { ( 1 p ) = 1 ① ( − 1 p ) = ( − 1 ) p − 1 2 ② ( 2 p ) = ( − 1 ) p 2 − 1 8 ③ ( q p ) = ( − 1 ) q − 1 2 p − 1 2 ( p q ) ④
\begin{cases}
(\frac{1}{p}) = 1&①\\
(\frac{-1}{p}) = (-1)^{\frac{p-1}{2}}&②\\
(\frac{2}{p}) = (-1)^{\frac{p^2-1}{8}}&③\\
(\frac{q}{p}) = (-1)^{\frac{q-1}{2}\frac{p-1}{2}}(\frac{p}{q})&④
\end{cases}
⎩ ⎨ ⎧ ( p 1 ) = 1 ( p − 1 ) = ( − 1 ) 2 p − 1 ( p 2 ) = ( − 1 ) 8 p 2 − 1 ( p q ) = ( − 1 ) 2 q − 1 2 p − 1 ( q p ) ① ② ③ ④
这个符号存在的意义是可以对未知的二次剩余进行简化或者通过已知的二次剩余推到未知的二次剩余关系
( 15 227 ) = ( 3 227 ) ( 5 227 ) = ( − 1 ) 113 × 1 ( 227 3 ) ( − 1 ) 113 × 2 ( 227 5 )
(\frac{15}{227}) = (\frac{3}{227})(\frac{5}{227}) = (-1)^{113\times1}(\frac{227}{3})(-1)^{113\times2}(\frac{227}{5})
( 227 15 ) = ( 227 3 ) ( 227 5 ) = ( − 1 ) 113 × 1 ( 3 227 ) ( − 1 ) 113 × 2 ( 5 227 ) − ( 227 3 ) ( 227 5 ) = − ( 2 3 ) ( 2 5 )
-(\frac{227}{3})(\frac{227}{5}) = -(\frac{2}{3})(\frac{2}{5})
− ( 3 227 ) ( 5 227 ) = − ( 3 2 ) ( 5 2 ) 2 3 − 1 2 ≡ − 1 m o d 3 2 5 − 1 2 ≡ − 1 m o d 3
2^{\frac{3-1}{2}}\equiv -1\,mod\,3\quad 2^{\frac{5-1}{2}}\equiv -1\,mod\,3
2 2 3 − 1 ≡ − 1 m o d 3 2 2 5 − 1 ≡ − 1 m o d 3 ( 15 227 ) = − ( 2 3 ) ( 2 5 ) = − 1 × ( − 1 ) × ( − 1 ) = − 1
(\frac{15}{227})=-(\frac{2}{3})(\frac{2}{5}) = -1\times(-1)\times(-1) = -1
( 227 15 ) = − ( 3 2 ) ( 5 2 ) = − 1 × ( − 1 ) × ( − 1 ) = − 1
Jacobi 符号 是 Legendre 的推广,在 Legendre 符号中,要求分母的模数 p 必须是一个奇素数,而在 Jacobi 符号中,取消了这种限制,即 m 可以为任意数
通过对 m 标准分解,可以将 Jacobi 符号转化为多个 Legendre 符号的乘法
( a m ) = ( a p 1 ) ( a p 2 ) . . . ( a p n )
(\frac{a}{m}) = (\frac{a}{p_1})(\frac{a}{p_2})...(\frac{a}{p_n})
( m a ) = ( p 1 a ) ( p 2 a ) ... ( p n a )
当 Jacobi 符号取消了奇素数的限制后,自然无法对二次剩余的所有情况进行判定
当 (a/m) = 1 时,什么也不能说明 当 (a/m) = -1 时,说明 a 是 模 m 的二次非 剩余 可以说 Legendre 是 Jacobi 的一种特殊情况
Rabin 加密算法 根据二次剩余进行加密和解密
为什么所选取的大素数 p 和 q 必须是模四余三的形式?
取大素数 p、q,计算模数 n = p x q
加密过程很简单,就是一个模平方运算,设明文为 m,则密文 c 为
c ≡ m 2 m o d n
c \equiv m^2\,mod\,n
c ≡ m 2 m o d n x 2 ≡ c m o d n
x^2\equiv c\,mod\,n
x 2 ≡ c m o d n
第一步:求解大素数 p 和 q 相互模的逆元 s 和 t,即求解
p s + q t = 1
ps+qt = 1
p s + qt = 1
第二步:求解两个基本根 u 和 v,用以下公式
u = c p + 1 4 m o d p v = c q + 1 4 m o d q
u = c^{\frac{p+1}{4}}\,mod\,p\quad v = c^{\frac{q+1}{4}}\,mod\,q
u = c 4 p + 1 m o d p v = c 4 q + 1 m o d q
第三步:求解同余方程的四个根
x = ( ± p s v ± q t u ) m o d n
x = (\pm\,psv\pm\,qtu)\,mod\,n
x = ( ± p s v ± qt u ) m o d n
可以注意到这四个根中,有两对互为相反数
x 1 = p s v + q t u = − ( p s v + q t u ) = − x 2 x 3 = p s v − q t u = q t u − p s v = − x 4
x_1=psv+qtu=-(psv+qtu)=-x_2\\
x_3=psv-qtu=qtu-psv=-x_4
x 1 = p s v + qt u = − ( p s v + qt u ) = − x 2 x 3 = p s v − qt u = qt u − p s v = − x 4 x 1 + x 2 = n x 3 + x 4 = n
x_1+x_2 = n\quad x_3+x_4 = n
x 1 + x 2 = n x 3 + x 4 = n