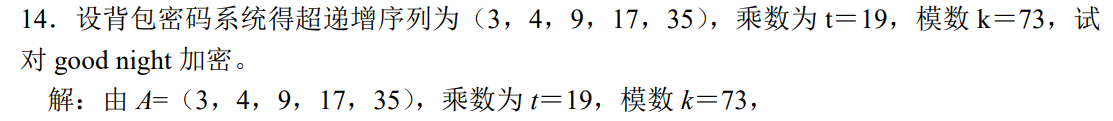公钥密码 northboat 8/21/2023 Cryptography
非对称加密,加密使用公钥,解密使用私钥
RSA 算法 大整数素数分解困难
RSA 的加密解密 两个大素数 p、q,其积记为 n,找到一个和 φ(n) 互素的整数 d
d ∈ ( 1 , φ ( n ) )
d\in(1,φ(n))
d ∈ ( 1 , φ ( n )) e = d − 1 ( m o d φ ( n ) )
e = d^{-1}(mod\,φ(n))
e = d − 1 ( m o d φ ( n ))
加密解密过程如下,设明文为 m,密文为 c
c ≡ m d m o d n
c\equiv m^d\,mod\,n
c ≡ m d m o d n m ≡ c e m o d n
m\equiv c^e\,mod\,n
m ≡ c e m o d n c e ≡ m d e = m
c^e\equiv m^{de}=m
c e ≡ m d e = m
RSA 的孙子定理优化 通过重复平方法的中间过程分解 n 背包密码体制 背包密码加密 超递增序列 A,乘数 k,模数 p,背包向量 B
注意背包向量的长度应等于每组的比特数,在背包体制中,每个字母为一个 5 位的二进制数,空格为 00000,A 为 00001,以此类推(背包长度和待加密分组的比特位数相同)
若背包向量 A 长度为 5,则每次处理一个字母,若为 10,则每次处理两个字母,若为 15 则每次处理三个字母......
背包密码的处理方式有点像独热码,如 c 表示 3,二进制为 00011,则其密文为
因为 c 的二进制在第四第五位取 1
举个栗子
背包密码解密 解密需要用到乘数 k 和模数 p(在背包体制中也是作为私钥,序列 B 作为公钥)
解密分为以下三步,
首先求 k 关于 p 的逆,记为 d 第二将已知的密文乘以 d 再模上 p,得到经过 A 加密后的明文 最后根据超递增序列 A,通过贪心算法构造二进制数得到明文 注意在已知 B 的情况下不能使用贪心算法,他不是超递增的,不满足最优子结构(这也符合公钥体制的设计思想,无法根据公钥解密)
举个栗子
Rabin 密码体制 大素数分解困难
Rabin 的加密解密 基于二次同余方程,模数 n 为两个大素数 p 和 q 之积
明文为 m,加密为
c ≡ m 2 m o d n
c\equiv m^2\,mod\,n
c ≡ m 2 m o d n x 2 ≡ c m o d n
x^2\equiv c\,mod\,n
x 2 ≡ c m o d n
求解二次同余方程的四个根(当 p 和 q 均模 4 得 3 时)
孙子定理 当知道二次同余方程的四个根 x1、x2、y1、y2 之后,这个二次同余方程转化为一个一次同余方程组
{ m ≡ x 1 m o d p m ≡ x 2 m o d p m ≡ y 1 m o d q m ≡ y 2 m o d q
\begin{cases}
m\equiv x_1\,mod\,p\\
m\equiv x_2\,mod\,p\\
m\equiv y_1\,mod\,q\\
m\equiv y_2\,mod\,q
\end{cases}
⎩ ⎨ ⎧ m ≡ x 1 m o d p m ≡ x 2 m o d p m ≡ y 1 m o d q m ≡ y 2 m o d q
椭圆曲线密码体制 椭圆曲线的嵌入和倍点运算 将明文 m 表示为椭圆曲线上的一个点 (m', f(m'))
m' 为 m 的线性变换,乘以 k 加上 j(一般 k 在 30-50 之间) f 为椭圆曲线函数,最后结果要模上模数 p 椭圆曲线表示为
G p ( a , b ) : f ( x ) = x 3 + a x + b m o d p
G_{p}(a,b):f(x)=x^3+ax+b\,mod\,p
G p ( a , b ) : f ( x ) = x 3 + a x + b m o d p
Diffie-Hellman 密码交换 a 是大素数的一个本原根
K = Y B X B = Y A X A = a X A X B
K=Y_B^{X_B}=Y_A^{X_A}=a^{X_AX_B}
K = Y B X B = Y A X A = a X A X B Y B = a X B Y A = a X A
Y_B=a^{X_B}\quad Y_A=a^{X_A}
Y B = a X B Y A = a X A a X B a X A
a^{X_B}\quad a^{X_A}
a X B a X A
在椭圆曲线上的实现
ElGamal 密码体制 重点,出计算
离散对数求解困难
ElGamal 的加密解密 选取大素数 p,随机数 g 和 x,计算
y ≡ g x m o d p
y \equiv g^x\,mod\,p
y ≡ g x m o d p
设明文为 M,选取任一与 p-1 互素的整数 k,加密过程为
C 1 = g k m o d p C 2 = y k M m o d p
C_1=g^k\,mod\,p\quad C_2=y^kM\,mod\,p
C 1 = g k m o d p C 2 = y k M m o d p M = C 2 C 1 x m o d p
M = \frac{C_2}{C_1^x}\,mod\,p
M = C 1 x C 2 m o d p C 2 C 1 x = y k M g x k = y k M y k = M m o d p
\frac{C_2}{C_1^x}=\frac{y^kM}{g^{xk}}=\frac{y^kM}{y^k}=M\,mod\,p
C 1 x C 2 = g x k y k M = y k y k M = M m o d p
ElGamal 的椭圆曲线实现 在椭圆曲线上的实现
在椭圆曲线上,倍点运算就相当于指数运算,其反向求解过程即为求解离散对数问题