单选（2/30）

1.算法的时间复杂度与（）有关

• A.问题规模
• B.计算机硬件的运行速度
• C.源程序的长度
• D.编译后执行程序的质量

2.向一个有 n 个元素的顺序表中插入一个新元素并保持原来顺序不变，则平均要移动（）个元素

• A.n
• B.n/2
• C.2n
• D.n^2

3.设指针变量 p 指向单链表中结点 A，若除单链表中结点 A，则需要修改指针的操作序列为（）

• A.q=p->next; p->data=q-data; p->next=q->next; free(q);
• B.q=p->next; q->data=p->data; p->next=q->next; free(q);
• C.q=p->next; p->next=q->next; free(q);
• D.q=p->next; p->data=q->data; free(q);

4.双向链表中有 2 个指针域 pre 和 next，分别指向直接前驱和直接后继，假设有指针 p 指向链表中的一个结点，指针 q 指向一个待插入的结点，则正确的在结点 p 之前插入结点 q 的语句为（）

• A.p->pre->next=q; q->next=p; q->pre=p->pre; p->pre=q;
• B.p->pre=q; q->next=p;q-pre-p-pre;p->pre=q;
• C.q->pre=p->pre; p->pre->next=q; q->next=p; p->pre=q->next;
• D.q-next=p; p->next=q; p->pre->next=q; q->next=p;

5.已知栈的最大容量是 4，若进栈顺序为 ABCDEF，则可能的出栈顺序列为（）

• A.CBEDAF
• B.BCEFAD
• C.ADFEBC
• D.EDCBAF

6.循环队列存储在数组A[0...m]中，入队时的操作为（）

• A.rear = rear+1

• C.rear = (rear+1) % (m+1)

• B.rear = (rear+1) % m

• D.rear = (rear+1) % (m-l)

7.假设用数组A[50]存放循环队列元素，头尾指针 front 和 rear，front=13， rear=5 时循环队列中元素的个数为（）

• A.42

• B.8

• C.43

• D.9

8.设串 s1=“ABCDEFG”，s2=“PQRST” 函数 Con(x, y) 返回 x 和 y 串的连接串，函数 Subs(s, i, j) 返回串 s 的从序号 i 开始的 j 个字符的子串，len(s) 返回串 s 的长度，则 Con(Subs(s1, 2, len(s2)), Subs(s1, len(s2), 2)) 的结果串是（）

• A.BCDEF
• B.BCDEFG
• C.BCPORST
• D.BCDEFEF

9.设矩阵A是一个对称矩阵，为了节省存储，将其下三角部分(如图所示)按行序存放在一维数组B[1...(n-1)/2]中，对下三角部分中任一元素a[i][j] (i<j)，在一维数组 B 中下标 k 的值是（）

• A.i(i-1)/2+j-1
• B.i(i-1)/2+j
• C.i(i+1)/2+j-1
• D.i(i+1)/2+j

10.假设一个电报使用 5 种字母组成，字母出现频率分别为 2、4、5、7、8，用这 5 个字母设计的哈夫曼树带权路径长度为（）

• A.10
• B.96
• C.84
• D.58

11.一个完全二叉树的第 6 层有 9 个叶子结点，则这颗二叉树最多有多少个结点（）

• A.41
• B.109
• C.40
• D.119

12.带权有向图 G 用邻接矩阵 A 存储，则顶点的入度等于 A 中（）

• A.第i行非0的元素之和
• B.第i列非0元素之和
• C.第i行非无穷且非0元素的个数
• D第i列非无穷且非0元素的个数

13.设 N 个点 E 条边的图用邻接表存，则求每个顶点入度的时间复杂度为（）

• A.O(N)
• B.O(N^2)
• C.O(N+E)
• D.O(N*E)

14.对序列 (15，9，7，8，20，1，4) 用快速排序方法升序排序，经过一趟排序后序列为（）

• A.9，7，8，4，1，15，20
• B.4，9，7，8，1，15，20
• C.1，9，7，8，4，15，20
• D.以上都不对

15:对包含 n 个元素的散列表进行查找，平均查找长度（）

• A.为 O(logn)
• B.为 O(n)
• C.与 n 无关
• D.与装填因子有关

判断（1/15）

1.运算的定义依赖于逻辑结构，运算的实现也依赖于逻辑结构而与存储结构无关（）

2线性表的各种基本运算在顺序存储结构上的实现均比在链式存储结构上的实现效率要低（）

3.线性表中的所有元素都有一个前驱元素和后继元素（）

4.删除栈底元素是栈的基本操作（）

5.队列和栈都是运算受限的线性表，只允许在表的两端进行运算（）

6.设串 S 的长度为 n，则 S 的子串个数最多为 n(n+1)/2（）

7.给定串 S1和 S2 的度分别为 n、m，则针对 S1、S2 使用布鲁特-福斯算法在最好情况下的时间复杂度为 O(n+m)（）

8.在完全二叉树中，叶子结点的双亲的左兄弟(如果存在)一定不是叶子结点（）

9.完全二叉树中不适合顺序存储结构，只有满二叉树适合顺序存储结构（）

10.在完全二叉树中，若一个结点没有左孩子，则它必是叶子结点（）

11.在一个图中，所有顶点的度数之和等于所有边的数目的 2 倍（）

12.所有边的权值都不相同的带权无向图的最小生成树是唯一的（）

13.在一个有向图中，所有顶点的入度之和等于所有顶点的出度之和（）

14.二分查找中，表必须有序，表可以顺序方式存储，也可以链表方式存储（）

15.若在散列表中删除一个元素，不能简单地将该元素删除（）

填空（2/30）

1.在最坏情况下的时间复杂度是（）

2.一个顺序表的第一个元素的存储地址是 0xl1f7c每个元素的长度为 4，则第 5 个元素的地址是（）

3.单链表中逻辑上相邻的元素，其物理位置（）相邻

4.线性表 (a1, a2...an) 以单链表方式时，访第 i 个位置的素的时间复度为（）

5.若一个的输入序列是 123...n，输出的第一个是 n，则第 i 个输出元素是（）

6.在用单链表实现队列时，队头在链表的（）位置

7.假设循环单链表表示的队列长度为 ，队头固定在链表表尾，若只设头指针，则入队操作的时间复杂度为（）

8.数组A[1...5][1...6]的每个元素占 5 个单元，将其按行优先顺序存储在起始地址为 1000 的连续内存单元中，则元素 A[5][5] 的地址为（）

9.设目标 T=“abccdcdccbaa”，模式 P=cdcc”，则第（）匹配成功

10.假定一颗度为 3 的树中结点数为 50，则其最小高度为（）

11.已知一颗二叉树的后序历序列为 DABEC，中序遍历序列为 DEBAC，则先序遍历序列为（）

12.一颗哈夫曼树共有 215 个结点，对其进行哈夫曼编码，共能得到不同的码字数量为（）

13.一个具有 n 个顶点e条边的有向图的邻接矩阵中，零元素的个数为（）

14.具有 n 个顶点的有向图最多可包含的有向边的条数是（）

15.已知一个有序表 (13，18，24，35，47，50，62，83，90，115，134)，当二分查找值为 90 的元素时，查找成功的比较次数为（）

问题求解（45）

1.(7分) 有5个元素，其入栈次序为 A、B、C、D、E，在各种出次序中，第一个出栈元素是 C 且第二个出栈元素为 D 的出栈序列有哪几个？

2.(7分) 一颗高度为 h 的满 m 树 (m 可以为2)有如下性质：根结点所在层次为第 1 层，第 h 层上的结点都是叶子结点，其余各层上每层结点都有 m 棵非空子树，如果按照层次自顶向下、同一层自左向右的顺序从 1 开始对全部结点进行编号，问

• (1) 各层的结点个数是多少？
• (2) 编号为 i 的结点的双亲结点(若存在)的编号是多少？

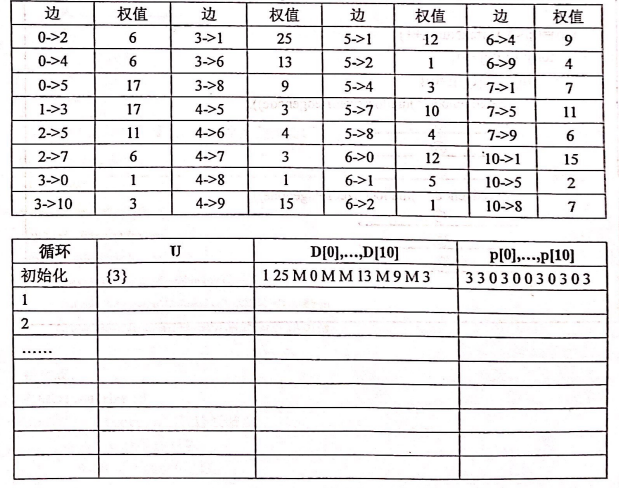
3.(8分) 已知某有向带权图 11 个节点的连接方式如下表示，以节点3为出发点，使用 Diikstra 算法求其最短路径并写出其动态执行情况，填写下表，其中 U 表示选定的节点集合，D[i]表示源点到节点i的距离，p[i]表示源点到节点 i 时，节点 i 的前驱节点

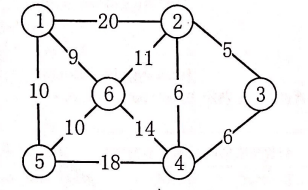
4.(8分) 已知一个无向图如下图所示，给出从顶点 1 出发用 kruskal 算法生成所有可能的最小生成树的过程

5.(7分) 设散列表的度为 15，散列函数为 H(k) = k%13，给定的关键序列为19，14，23，01，68，20，84，27，55，11，10，79。试画出用线性探查法解决冲突时所构造的散列表，并求出在等概率情况下，这种方法的查找成功和查找不成功的平均查找长度

6.(8分) 已知序列 (503，87，512，61，908，170，897，275，653，462)，采用二路归并排序法对其进行排序，并写出排序过程

算法设计（30）

1.(10分) 设计一个算法，将表中所有节点的方向“原地旋转”，要求利用原表的存储空间。例如：L = {0，2，4，6，8，10}，逆转后为 L = (10，8，6，4，2，0}

void Inverse(LinkList *L){
    LinkList p, q;
    ____①____
    L->next = NULL;
    while(____②____){
        q = p->next;
        ____③____;
        ____④____;
        ____⑤____;
    }
}

2.(10分) 请写出先序遍历的非递归算法

typedef struct TreeNode{
    int data;
    struct TreeNode *lChild;
    struct TreeNode *rChild;
}TreeNode;

void preOrder (TreeNode *T){
    TreeNode *stack [15];
    int top = -l;
    TreeNode*p = T;
    while(____①____){
        if(p != NULL){
            stack[____②____] = p; // 进栈
            printf("%d\t", p->data); // 入栈时，访问输出
            p = ____③____;
        } else {
            p = stack[____④____]; // 出栈
            p = ____⑤____;
        }
    }
}

3.(10分) 设计一个算法，将一个无向图的邻接矩阵转换为邻接表。已知邻接矩阵和邻接，表的结构定义如下

// 邻接矩阵
#define Maxsize 10
tpyedef char vextype;
struct AdjMatrix{
    vextype vexs[Maxsize];//存放顶点的数组
    int arc[Maxsize][Maxsize];//存放边的数组
    int vertexNum, arcNum;//图的顶点和边数
}

// 邻接表
#define Maxsize 10
typedef struct node{ //邻接链表结点
    int adjvex;//邻接点域
    struct node *next;//链域
}edgenode;

typedef struct{
    vextype vertex;//顶点域
    edgenode *link;//指针域
}vexnode;

struct AdjList{
    vexnode adjlist[Maxsize]:
    int vertexNum, arcNum;//图的顶点和边数
};

补全如下程序，完成邻接矩阵转为邻接表算法

void MatToList(struct AdjMatrix A, struct AdjList B){
    B.vertexNum = ____①____;
    B.arcNum = ____②____;
    for(i = 0; i < A.vertexNum; i++){
        B.adjlist[i].vertex = ____③____;
        ____④____;
    }
    for(i = 0; i < A.vertexNum; i++){
        for(j = 0; j < i; j++){
            if(A.arc[i][i] != 0){
                p=(edgenode*)malloc(sizeof(edgenode)):
                ____⑤____;
                ____⑥____;
                ____⑦____;
                p=(edgenode*)malloc(sizeof(edgenode));
                ____⑧____;
                ____⑨____;
                ____⑩____;
            }
        }
    }
}